题目内容
15.为了解某地高一年级男生的身高情况,从其中的一个学校选取容量为60的样本(60名男生的身高,单位:cm),分组情况如表:| 分组 | 151.5~158.5 | 158.5~165.5 | 165.5~172.5 | 172.5~179.5 |
| 频数 | 6 | 21 | 27 | 6 |
| 频率 | 0.1 | 0.35 | a | 0.1 |
分析 根据频率=频数÷样本容量,计算出第二列、第三列的频率,第五列的频数,然后根据样本容量为60,可知第四列的频数为27,进而算出a的值.
解答 解:151.5~158.5范围内的频率为:6÷60=0.1,
158.5~165.5范围内的频率为:21÷60=0.35,
172.5~179.5范围内的频数为:0.1×60=6,
所以165.5~172.5范围内的频数为:60-6-21-6=27,故其频率a=27÷60=0.45
故答案为:0.45
点评 本题考查了频率=频数÷样本容量的公式,属于基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
5.在等差数列{an}中,3(a3+a5)+2(a7+a10+a13)=24,则此数列前13项之和为( )
| A. | 126 | B. | 26 | C. | 13 | D. | 12 |
20.复数$\frac{i-1}{i}$(i是虚数单位)在复平面上对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的一个焦点与抛物线y2=4$\sqrt{10x}$的焦点重合,且双曲线的离心率等于$\frac{{\sqrt{10}}}{3}$,则该双曲线的方程为( )
| A. | x2-$\frac{y^2}{9}$=1 | B. | x2-y2=15 | C. | $\frac{x^2}{9}-{y^2}$=1 | D. | x2-y2=9 |
17.执行如图所示的程序框图,则输出的结果为( )
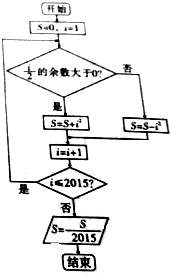

| A. | 1006 | B. | 1008 | C. | 2015 | D. | 2016 |