题目内容
4．△ABC的顶点A在圆O：x2+y2=1上，B，C两点在直线$\sqrt{3}$x+y+3=0上，若|$\overrightarrow{AB}$-$\overrightarrow{AC}$|=4，则△ABC面积的最小值为1．分析 求出圆上点到直线距离的最小值，|BC|=4，即可求出△ABC面积的最小值．
解答 解：由题意，|BC|=4，圆心到直线的距离d=$\frac{3}{\sqrt{3+1}}$=$\frac{3}{2}$，
∴圆上点到直线距离的最小值为$\frac{1}{2}$，
∴△ABC面积的最小值为$\frac{1}{2}×4×\frac{1}{2}$=1．
故答案为：1．
点评 本题考查直线与圆的位置关系，考查三角形面积的计算，求出圆上点到直线距离的最小值是关键．
练习册系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
15．为了解某地高一年级男生的身高情况，从其中的一个学校选取容量为60的样本（60名男生的身高，单位：cm），分组情况如表：
则表中的a=0.45．
| 分组 | 151.5～158.5 | 158.5～165.5 | 165.5～172.5 | 172.5～179.5 |
| 频数 | 6 | 21 | 27 | 6 |
| 频率 | 0.1 | 0.35 | a | 0.1 |
12．
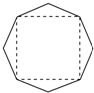某班设计了一个八边形的班徽（如图），它由腰长为1，顶角为α的四个等腰三角形，及其底边构成的正方形所组成．该八边形的面积为（ ）
某班设计了一个八边形的班徽（如图），它由腰长为1，顶角为α的四个等腰三角形，及其底边构成的正方形所组成．该八边形的面积为（ ）| A． | 2sin α-2cos α+2 | B． | sin α-$\sqrt{3}$cos α+3 | C． | 3sin α-$\sqrt{3}$cos α+1 | D． | 2sin α-cos α+1 |
19．已知函数f（x）=cos（2x+$\frac{π}{3}$），g（x）=sin（2x+$\frac{2π}{3}$），将f（x）的图象经过下列哪种变换可以与g（x）的图象重合（ ）
| A． | 向左平移$\frac{π}{12}$ | B． | 向右平移$\frac{π}{12}$ | C． | 向左平移$\frac{π}{6}$ | D． | 向右平移$\frac{π}{6}$ |
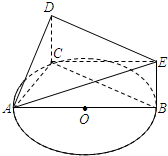如图，AB是圆O的直径，C是圆O上异于A，B的一个动点，DC垂直于圆O所在的平面，DC∥EB，DC=EB=1，AB=4．