题目内容
20．复数$\frac{i-1}{i}$（i是虚数单位）在复平面上对应的点位于（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 利用复数的运算法则、几何意义即可得出．
解答 解：复数$\frac{i-1}{i}$=$\frac{-i（i-1）}{-i•i}$=1+i在复平面上对应的点（1，1）位于第一象限，
故选：A．
点评 本题考查了复数的运算法则、几何意义，属于基础题．
练习册系列答案
相关题目
10．已知角α的终边上一点P落在直线y=2x上，则sin2α=（ ）
| A． | $-\frac{{2\sqrt{5}}}{5}$ | B． | $\frac{{2\sqrt{5}}}{5}$ | C． | $-\frac{4}{5}$ | D． | $\frac{4}{5}$ |
15．为了解某地高一年级男生的身高情况，从其中的一个学校选取容量为60的样本（60名男生的身高，单位：cm），分组情况如表：
则表中的a=0.45．
| 分组 | 151.5～158.5 | 158.5～165.5 | 165.5～172.5 | 172.5～179.5 |
| 频数 | 6 | 21 | 27 | 6 |
| 频率 | 0.1 | 0.35 | a | 0.1 |
5．若直线2ax-by+2=0（a＞0，b＞0）被圆x2+y2+2x-4y+1=0截得的弦长为4，则$\frac{1}{a}+\frac{1}{b}$的最小值是（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | -2 | D． | 4 |
12．
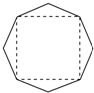某班设计了一个八边形的班徽（如图），它由腰长为1，顶角为α的四个等腰三角形，及其底边构成的正方形所组成．该八边形的面积为（ ）
某班设计了一个八边形的班徽（如图），它由腰长为1，顶角为α的四个等腰三角形，及其底边构成的正方形所组成．该八边形的面积为（ ）| A． | 2sin α-2cos α+2 | B． | sin α-$\sqrt{3}$cos α+3 | C． | 3sin α-$\sqrt{3}$cos α+1 | D． | 2sin α-cos α+1 |