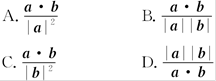题目内容
已知a,b,c是平面向量,下列命题中真命题的个数是( )
①(a·b)·c=a·(b·c);
②|a·b|=|a|·|b|;
③|a+b|2=(a+b)2;
④a·b=b·c ⇒a=c
①(a·b)·c=a·(b·c);
②|a·b|=|a|·|b|;
③|a+b|2=(a+b)2;
④a·b=b·c ⇒a=c
| A.1 | B.2 | C.3 | D.4 |
A
对于①,因为a·b,b·c是两个数,显然,(a·b)·c=a·(b·c)不一定恒成立;对于②,因为|a·b|=|a|·|b|·|cosθ|,显然也不恒成立;对于④,由于a·b与b·c是两个具体的数,由两个数不可能产生两个向量相等,于是也不正确;而对于③,由于|a+b|2=a2+2a·b+b2,而(a+b)2=a2+2a·b+b2,显然二者是相等的.故选A.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
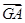 +
+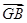 +
+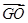 ;
;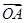 =a,
=a,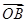 =b,
=b,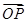 =ma,
=ma,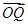 =nb,求证:
=nb,求证: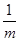 +
+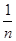 =3.
=3.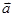 =(cos
=(cos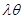 ,cos(
,cos(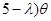 ),
),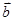 =(
=(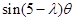 ,sin
,sin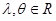
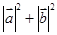 的值;
的值;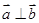 ,求
,求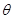 ;
;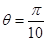 ,求证:
,求证: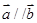 .
.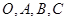 满足向量
满足向量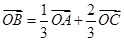 ,则
,则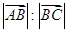 等于( )
等于( )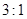
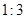
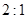

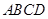 的边长为
的边长为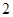 ,
,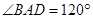 ,点
,点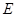 ,
,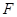 分别在边
分别在边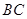 、
、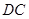 上,
上,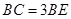 ,
,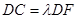 .若
.若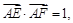 ,则
,则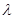 的值为________.
的值为________. cosx-sinx),n=(sin(x+
cosx-sinx),n=(sin(x+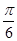 ),sinx),且满足f(x)=m·n.
),sinx),且满足f(x)=m·n.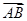 ·
·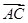 =
=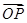 =
=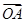 +t
+t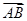 ,试问:
,试问: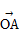 =a,
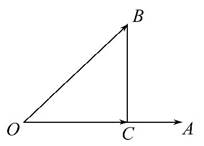
=a,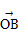 =b,且BC⊥OA,C为垂足,若
=b,且BC⊥OA,C为垂足,若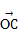 =λa(λ≠0),则λ=( )
=λa(λ≠0),则λ=( )