题目内容
已知点G是△ABO的重心,M是AB边的中点.
(1)求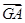 +
+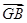 +
+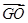 ;
;
(2)若PQ过△ABO的重心G,且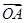 =a,
=a,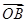 =b,
=b,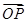 =ma,
=ma,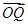 =nb,求证:
=nb,求证: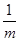 +
+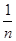 =3.
=3.
(1)求
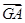 +
+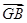 +
+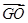 ;
;(2)若PQ过△ABO的重心G,且
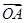 =a,
=a,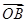 =b,
=b,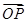 =ma,
=ma,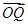 =nb,求证:
=nb,求证: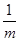 +
+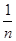 =3.
=3.(1)0 (2)见解析
解:(1)∵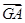 +
+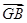 =2
=2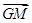 ,又2
,又2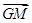 =-
=-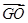 ,
,
∴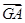 +
+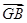 +
+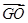 =-
=-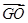 +
+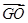 =0.
=0.
(2)证明:显然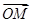 =
=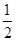 (a+b).
(a+b).
因为G是△ABO的重心,
所以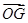 =
=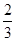
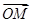 =
=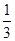 (a+b).
(a+b).
由P,G,Q三点共线,得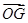 =t
=t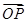 +(1-t)
+(1-t)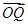 ,
,
即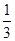 a+
a+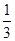 b=mta+(1-t)nb,
b=mta+(1-t)nb,
由a,b不共线,得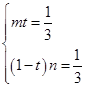
∴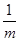 +
+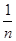 =3.
=3.
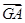 +
+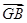 =2
=2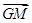 ,又2
,又2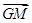 =-
=-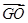 ,
,∴
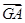 +
+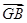 +
+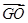 =-
=-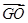 +
+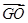 =0.
=0.(2)证明:显然
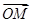 =
=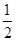 (a+b).
(a+b).因为G是△ABO的重心,
所以
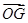 =
=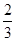
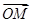 =
=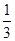 (a+b).
(a+b).由P,G,Q三点共线,得
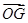 =t
=t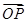 +(1-t)
+(1-t)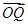 ,
,即
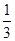 a+
a+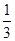 b=mta+(1-t)nb,
b=mta+(1-t)nb,由a,b不共线,得
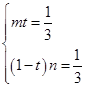
∴
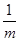 +
+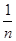 =3.
=3.
练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
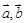 满足
满足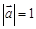 ,且
,且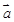 与
与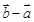 的夹角为
的夹角为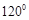 ,则
,则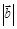 的取值范围为 。
的取值范围为 。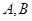 是锐角
是锐角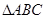 的两内角,
的两内角,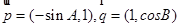 ,则
,则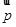 与
与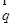 的夹角是( )
的夹角是( )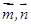 满足:对任意的
满足:对任意的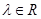 ,恒有
,恒有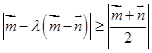 ,则( )
,则( )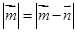
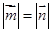
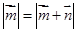
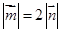
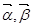 是一组基底,向量
是一组基底,向量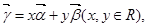 则称
则称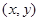 为向量
为向量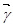 在基底
在基底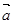 在基底
在基底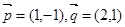 下的坐标为
下的坐标为 ,则向量
,则向量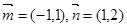 下的坐标为( ).
下的坐标为( ).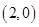
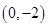
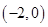
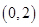
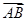 =λ
=λ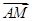 +μ
+μ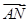 ,则λ+μ=( )
,则λ+μ=( )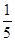 B.
B.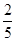 C.
C.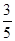 D.
D.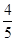
 ,则
,则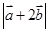 的值为 .
的值为 .