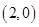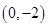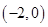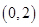题目内容
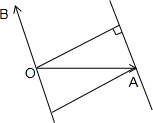
已知|
|=4,|
|=6,
=x
+y
,且x+2y=1,∠AOB是钝角,若f(t)=|
-t
|的最小值为2
,则|
|的最小值是______.
| OA |
| OB |
| OC |
| OA |
| OB |
| OA |
| OB |
| 3 |
| OC |
f(t)=|
-t
|的最小值为2
,
∴根据图形知,当
-t
⊥
时,f(t)=|
-t
|的最小值为2
,
∵|
|=4,∴∠AOB=120°,
∵
=x
+y
,且x+2y=1,
∴|
|2=x2
2+y2
2+2xy
•
=16x2+36y2-24xy=16(1-2y)2+36y2-24(1-2y)y
=148y2-88y+16≥
.
∴|
|的最小值是
;
故答案为
.
| OA |
| OB |
| 3 |
∴根据图形知,当
| OA |
| OB |
| OB |
| OA |
| OB |
| 3 |
∵|
| OA |
∵
| OC |
| OA |
| OB |
∴|
| OC |
| OA |
| OB |
| OA |
| OB |
=16x2+36y2-24xy=16(1-2y)2+36y2-24(1-2y)y
=148y2-88y+16≥
| 108 |
| 37 |
∴|
| OC |
6
| ||
| 37 |
故答案为
6
| ||
| 37 |


练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
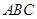 中,点
中,点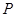 是
是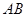 上一点,且
上一点,且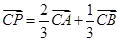 ,
,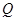 是
是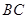 中点,
中点,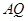 与
与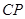 交点为
交点为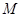 ,又
,又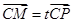 ,则
,则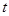 的值为( )
的值为( )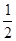
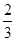
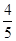
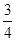
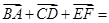 ( )
( )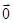
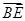
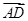
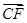
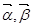 是一组基底,向量
是一组基底,向量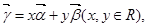 则称
则称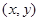 为向量
为向量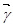 在基底
在基底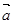 在基底
在基底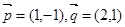 下的坐标为
下的坐标为 ,则向量
,则向量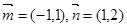 下的坐标为( ).
下的坐标为( ).