题目内容
2．已知函数f（x）=loga（x+1）（a＞0，a≠1）在[0，1]上的值域是[0，1]，若函数g（x）=ax-m-4的图象不过第二象限，则m的取值范围是（ ）| A． | [-2，+∞） | B． | [-$\frac{1}{2}$，+∞） | C． | [-1，+∞） | D． | （-∞，2] |
分析 对a分类讨论：利用对数函数的单调性可得a=2．由于函数g（x）=2x-m-4的图象不过第二象限，可得g（0）≤0，解出即可．
解答 解：当a＞1时，函数f（x）在[0，1]上单调递增，∴loga1=0，loga2=1，解得a=2．
当0＜a＜1时，函数f（x）在[0，1]上单调递减，∴loga1=1，loga2=0，舍去．
故a=2．
∵函数g（x）=2x-m-4的图象不过第二象限，
∴g（0）=2-m-4≤0，
∴-m≤2，
解得m≥-2．
故选：A．
点评 本题考查了指数函数与对数函数的单调性，考查了数形结合的思想方法、推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
13．设F1，F2为椭圆的两焦点，B为椭圆短轴的一个端点，若△BF1F2为正三角形，则椭圆的离心率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | 2 |
如图，已知直线a∥平面α，在平面α内有一动点P，点A是直线a上一定点，且AP与直线a所成角θ=$\frac{π}{4}$，点A到平面α的距离为2，若过点A作AO⊥α于点O，在平面α内，以过点O作直线a的平行线为x轴，以过点O作x轴的垂线为y轴建立直角坐标系，则动点P的轨迹方程为x2-y2=4．．
7．已知m、n是两条不同的直线，α、β是两个不同的平面，则下列命题正确的是（ ）
| A． | 若m∥n，m∥α且n∥β，则α∥β?????????? | |
| B． | 若m⊥n，m∥α且n∥β，则α⊥β? | |
| C． | 若m∥α且n⊥m，则n⊥α???????????????????? | |
| D． | 若m⊥n，m⊥α且n⊥β，则α⊥β |
14．一个几何体的三视图如图所示，则这个几何体的体积为（ ）
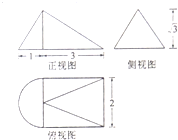
| A． | $\frac{（8+π）\sqrt{3}}{6}$ | B． | $\frac{（12+π）\sqrt{3}}{6}$ | C． | $\frac{（12+π）\sqrt{3}}{2}$ | D． | $\frac{（6+π）\sqrt{3}}{3}$ |
11．已知F1、F2是椭圆的两个焦点，以线段F1F2为边作正△MF1F2，若边MF1的中点在此椭圆上，则此椭圆的离心率为（ ）
| A． | $\frac{\sqrt{3}-1}{2}$ | B． | $\sqrt{2}$-1 | C． | $\frac{\sqrt{2}}{2}$ | D． | $\sqrt{3}$-1 |