题目内容
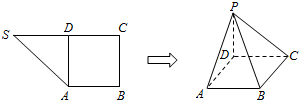
1.如图,在直角梯形SABC中,∠B=∠C=$\frac{π}{2}$,D为边SC上的点,且AD⊥SC,现将△SAD沿AD折起到达PAD的位置(折起后点S记为P),并使得PA⊥AB.(1)求证:PD⊥平面ABCD;
(2)已知PD=AD,PD+AD+DC=6,G是AD的中点,当线段PB取得最小值时,则在平面PBC上是否存在点F,使得FG⊥平面PBC?若存在,确定点F的位置,若不存在,请说明理由.
分析 (1)根据线面垂直的判定定理即可证明PD⊥平面ABCD;
(2)根据线面垂直的判定定理以及直线平行的性质进行证明即可.
解答 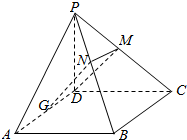 证明:(1)∵PA⊥AB,AB⊥AD,PA⊥AD=A,
证明:(1)∵PA⊥AB,AB⊥AD,PA⊥AD=A,
∴AB⊥平面PAD,
∵PD?平面PAD,
∴AB⊥PD,
∵PD⊥AD,AD∩AB=A,
∴PD⊥平面ABCD
(2)设PD=x,则AD=x,DC=6-2x,
∴PB2=x2+x2+(6-2x)2=6(x-2)2+12,当且仅当x=2时,PB2取得最小值,
即PB取得最小值,
取PC的中点M,PB的中点N,
则DM⊥平面PBC,
∵四边形DMNG是平行四边形,
∴GN∥DM,
GN⊥平面PBC,
∴在平面PBC上存在点F,即PB的中点,使FG⊥平面PBC.
点评 本题主要考查了线面垂直的定义和判定定理的应用,考查了学生对基础知识的综合运用.

练习册系列答案
相关题目
11.已知F1、F2是椭圆的两个焦点,以线段F1F2为边作正△MF1F2,若边MF1的中点在此椭圆上,则此椭圆的离心率为( )
| A. | $\frac{\sqrt{3}-1}{2}$ | B. | $\sqrt{2}$-1 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{3}$-1 |
9.下列各点中,在曲线x2-xy+2y+1=0上的点是( )
| A. | (2,-2) | B. | (4,-3) | C. | (3,10) | D. | (-2,5) |
16.如图,等腰三角形OAB(O为坐标原点)的顶点A,B的坐标分别为(6,0),(3,3),AB与直线y=$\frac{1}{2}$x交于点C,在△OAB中任取一点P,则点P落在△OBC中的概率( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
6.设条件p:a>0,条件q:a2+a>0; 那么p就是q的( )
| A. | 充要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
10.设函数f(x)=x4-ax(a>0)的零点都在区间[0,5]上,则函数g(x)=$\frac{1}{x}$与函数h(x)=x3-a的图象的交点的横坐标为正整数时,实数a的所有取值中最大值为( )
| A. | $\frac{80}{3}$ | B. | $\frac{255}{4}$ | C. | $\frac{624}{5}$ | D. | $\frac{1295}{6}$ |