题目内容
19.已知A,B是△ABC的两个内角,$\overrightarrow{a}$=($\sqrt{2}$cos$\frac{A+B}{2}$,sin$\frac{A-B}{2}$),若|$\overrightarrow{a}$|=$\frac{\sqrt{6}}{2}$.(1)求tanA•tanB的值;
(2)求tanC的最大值,并判断此时三角形的形状.
分析 (1)利用向量的模结合两角和与差的三角函数化简求解即可.
(2)利用两角和的正切函数,结合基本不等式求出最值,然后判断三角形的形状即可.
解答 解:(1)∵$|\vec a{|^2}=2{cos^2}\frac{A+B}{2}+{sin^2}\frac{A-B}{2}=\frac{3}{2}$,∴$1+cos(A+B)+\frac{1-cos(A-B)}{2}=\frac{3}{2}$;…(2分)
化简得 $cosAcosB-sinAsinB-\frac{cosAcosB+sinAsinB}{2}=0$,
所以,$\frac{1}{2}cosAcosB=\frac{3}{2}sinAsinB$,…(5分)
∴$tanAtanB=\frac{1}{3}$.…(6分)
(2)由(1)可知A,B为锐角,则tanA>0,tanB>0,…(7分)$tanC=-tan(A+B)=-\frac{tanA+tanB}{1-tanAtanB}=-\frac{3(tanA+tanB)}{2}≤-3\sqrt{tanAtanB}=-\sqrt{3}$.
(当且仅当tanA=tanB=$\frac{\sqrt{3}}{3}$,“=”成立) …(10分)
所以tanC的最大值为-$\sqrt{3}$,此时三角形的形状为等腰三角形.…(12分)
点评 本题考查三角形的解法,两角和与差的三角函数的应用,基本不等式的应用,考查计算能力.

练习册系列答案
相关题目
7.已知m、n是两条不同的直线,α、β是两个不同的平面,则下列命题正确的是( )
| A. | 若m∥n,m∥α且n∥β,则α∥β?????????? | |
| B. | 若m⊥n,m∥α且n∥β,则α⊥β? | |
| C. | 若m∥α且n⊥m,则n⊥α???????????????????? | |
| D. | 若m⊥n,m⊥α且n⊥β,则α⊥β |
14.一个几何体的三视图如图所示,则这个几何体的体积为( )
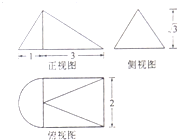

| A. | $\frac{(8+π)\sqrt{3}}{6}$ | B. | $\frac{(12+π)\sqrt{3}}{6}$ | C. | $\frac{(12+π)\sqrt{3}}{2}$ | D. | $\frac{(6+π)\sqrt{3}}{3}$ |
11.已知F1、F2是椭圆的两个焦点,以线段F1F2为边作正△MF1F2,若边MF1的中点在此椭圆上,则此椭圆的离心率为( )
| A. | $\frac{\sqrt{3}-1}{2}$ | B. | $\sqrt{2}$-1 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{3}$-1 |
8.对于集合M,定义函数fM(x)=$\left\{\begin{array}{l}{-1,x∈M}\\{1,x∉M}\end{array}\right.$,对于两个集合M、N,定义集合M⊕N={x|fM(x)•fN(x)=-1},已知A={2,4,6,8,10},B={1,2,4,5,6,8,9},则集合A⊕B=( )
| A. | {1,5,9,10} | B. | {1,5,9} | C. | {2,4,6} | D. | {2,4,6,8} |
9.下列各点中,在曲线x2-xy+2y+1=0上的点是( )
| A. | (2,-2) | B. | (4,-3) | C. | (3,10) | D. | (-2,5) |