题目内容
20.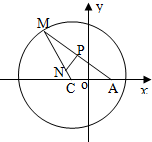 如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在线段AM上,点N在CM上,且满足$\overrightarrow{AM}$=2$\overrightarrow{AP}$,$\overrightarrow{NP}$•$\overrightarrow{AM}$=0,点N的轨迹为曲线E.求曲线E的方程.
如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在线段AM上,点N在CM上,且满足$\overrightarrow{AM}$=2$\overrightarrow{AP}$,$\overrightarrow{NP}$•$\overrightarrow{AM}$=0,点N的轨迹为曲线E.求曲线E的方程.
分析 通过向量关系,判断点N的轨迹为曲线E.满足椭圆定义,然后求解椭圆的方程即可.
解答  解:$\overrightarrow{AM}=2\overrightarrow{AP}$,$\overrightarrow{NP}•\overrightarrow{AM}=0$,
解:$\overrightarrow{AM}=2\overrightarrow{AP}$,$\overrightarrow{NP}•\overrightarrow{AM}=0$,
所以NP为线段AM的垂直平分线,|NA|=|NM|,
$|{NC}|+|{NA}|=|{NC}|+|{NM}|=2\sqrt{2}>2=|{CA}|$,
所以动点N的轨迹是以C(-1,0),A(1,0)为焦点的椭圆,…..(3分)
且长轴长为$2a=2\sqrt{2}$,焦距2c=2,所以$a=\sqrt{2}$,c=1,b2=1,
曲线E的方程为$\frac{x^2}{2}+{y^2}=1$.….(6分)
点评 本题考查椭圆的定义的应用,轨迹方程的求法,考查计算能力.

练习册系列答案
相关题目
11.已知F1、F2是椭圆的两个焦点,以线段F1F2为边作正△MF1F2,若边MF1的中点在此椭圆上,则此椭圆的离心率为( )
| A. | $\frac{\sqrt{3}-1}{2}$ | B. | $\sqrt{2}$-1 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{3}$-1 |
8.对于集合M,定义函数fM(x)=$\left\{\begin{array}{l}{-1,x∈M}\\{1,x∉M}\end{array}\right.$,对于两个集合M、N,定义集合M⊕N={x|fM(x)•fN(x)=-1},已知A={2,4,6,8,10},B={1,2,4,5,6,8,9},则集合A⊕B=( )
| A. | {1,5,9,10} | B. | {1,5,9} | C. | {2,4,6} | D. | {2,4,6,8} |
5.已知a∈R,复数i2-ai在复平面内对应的点在直线x-y=0上,则实数a的值是( )
| A. | 1 | B. | 0 | C. | -1 | D. | 2 |
9.下列各点中,在曲线x2-xy+2y+1=0上的点是( )
| A. | (2,-2) | B. | (4,-3) | C. | (3,10) | D. | (-2,5) |
10.设函数f(x)=x4-ax(a>0)的零点都在区间[0,5]上,则函数g(x)=$\frac{1}{x}$与函数h(x)=x3-a的图象的交点的横坐标为正整数时,实数a的所有取值中最大值为( )
| A. | $\frac{80}{3}$ | B. | $\frac{255}{4}$ | C. | $\frac{624}{5}$ | D. | $\frac{1295}{6}$ |