题目内容
如图所示,B(– c,0),C(c,0),AH⊥BC,垂足为H,且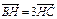 .
.
(1)若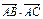 = 0,求以B、C为焦点并且经过点A的椭圆的离心率;
= 0,求以B、C为焦点并且经过点A的椭圆的离心率;
(2)D分有向线段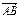 的比为
的比为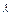 ,A、D同在以B、C为焦点的椭圆上,当 ―5≤
,A、D同在以B、C为焦点的椭圆上,当 ―5≤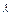 ≤
≤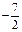 时,求椭圆的离心率e的取值范围.
时,求椭圆的离心率e的取值范围.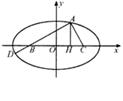
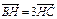 .
.(1)若
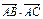 = 0,求以B、C为焦点并且经过点A的椭圆的离心率;
= 0,求以B、C为焦点并且经过点A的椭圆的离心率;(2)D分有向线段
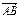 的比为
的比为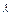 ,A、D同在以B、C为焦点的椭圆上,当 ―5≤
,A、D同在以B、C为焦点的椭圆上,当 ―5≤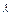 ≤
≤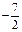 时,求椭圆的离心率e的取值范围.
时,求椭圆的离心率e的取值范围.
(1) .
.
(2) ≤e≤
≤e≤ .
.
 .
. (2)
 ≤e≤
≤e≤ .
.(1)因为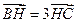 ,所以H
,所以H ,又因为AH⊥BC,所以设A
,又因为AH⊥BC,所以设A ,由
,由 得
得 即
即 3分
3分
所以|AB| =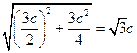 ,|AC | =
,|AC | =
椭圆长轴2a =" |AB|" + |AC| = (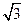 + 1)c, 所以,
+ 1)c, 所以, .
.
(2)设D (x1,y1),因为D分有向线段 的比为
的比为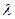 ,所以
,所以 ,
, ,
,
设椭圆方程为 =" 1" (a > b > 0),将A、D点坐标代入椭圆方程得
=" 1" (a > b > 0),将A、D点坐标代入椭圆方程得  .①
.①
 …………………………….. ②
…………………………….. ②
由①得
 ,代入②并整理得
,代入②并整理得 ,
,
因为 – 5≤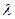 ≤
≤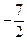 ,所以
,所以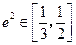 ,又0 < e < 1,所以
,又0 < e < 1,所以 ≤e≤
≤e≤ .
.
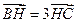 ,所以H
,所以H ,又因为AH⊥BC,所以设A
,又因为AH⊥BC,所以设A ,由
,由 得
得 即
即 3分
3分 所以|AB| =
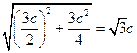 ,|AC | =
,|AC | =
椭圆长轴2a =" |AB|" + |AC| = (
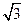 + 1)c, 所以,
+ 1)c, 所以, .
. (2)设D (x1,y1),因为D分有向线段
 的比为
的比为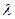 ,所以
,所以 ,
, ,
, 设椭圆方程为
 =" 1" (a > b > 0),将A、D点坐标代入椭圆方程得
=" 1" (a > b > 0),将A、D点坐标代入椭圆方程得  .①
.① …………………………….. ②
…………………………….. ②由①得

 ,代入②并整理得
,代入②并整理得 ,
, 因为 – 5≤
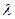 ≤
≤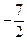 ,所以
,所以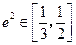 ,又0 < e < 1,所以
,又0 < e < 1,所以 ≤e≤
≤e≤ .
.
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
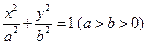 的左焦点
的左焦点 作x轴的垂线交椭圆于点P,点A和点B分别为椭圆的右顶点和上顶点,OP∥AB.
作x轴的垂线交椭圆于点P,点A和点B分别为椭圆的右顶点和上顶点,OP∥AB. (2)过右焦点
(2)过右焦点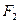 作一条弦QR,使QR⊥AB.若△
作一条弦QR,使QR⊥AB.若△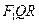 的面积为
的面积为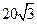 ,求椭圆的方程.
,求椭圆的方程.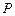 是椭圆
是椭圆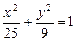 上的一点,
上的一点,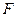 是椭圆的左焦点,且
是椭圆的左焦点,且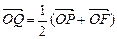 ,
,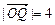 则点
则点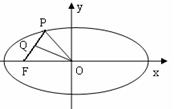
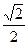 .
. .又AB的中点M与椭圆中心连线的斜率为
.又AB的中点M与椭圆中心连线的斜率为 ,求椭圆的方程.
,求椭圆的方程. ;②
;②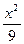 +
+ =1;?③x2+
=1;?③x2+ +y2=1.其中与直线x+y-5=0仅有一个交点的曲线是( )
+y2=1.其中与直线x+y-5=0仅有一个交点的曲线是( )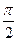 ),方程x2sinα+y2cosα=1表示焦点在y轴上的椭圆,则α的取值范围是______.
),方程x2sinα+y2cosα=1表示焦点在y轴上的椭圆,则α的取值范围是______.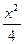 +y2=1的左、右焦点,点P在椭圆上运动,则|PF1|·|PF2|的最大值是_________________.
+y2=1的左、右焦点,点P在椭圆上运动,则|PF1|·|PF2|的最大值是_________________.