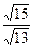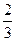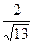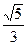题目内容
已知椭圆的中心在原点,焦点在x轴上,一个顶点A(0,-1),且右焦点到右准线的距离为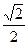 .
.
(1)求椭圆的方程.
(2)试问是否能找到一条斜率为k(k≠0)的直线l,使l与椭圆交于不同两点M、N且满足|AM|=|AN|?若这样的直线存在,求出k的取值范围;若不存在,请说明理由.
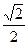 .
.(1)求椭圆的方程.
(2)试问是否能找到一条斜率为k(k≠0)的直线l,使l与椭圆交于不同两点M、N且满足|AM|=|AN|?若这样的直线存在,求出k的取值范围;若不存在,请说明理由.
1、椭圆方程为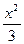 +y2=1.
+y2=1.
2、k∈(-1,0)∪(0,1).
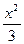 +y2=1.
+y2=1.2、k∈(-1,0)∪(0,1).
(1)设椭圆方程为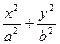 =1,由已知得b=1,
=1,由已知得b=1,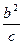 =
=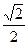 .
.
∴c=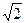 ,a2=3.
,a2=3.
∴椭圆方程为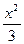 +y2=1.
+y2=1.
(2)设M(x1,y1)、N(x2,y2),MN中点P(x0,y0).
∴ 两式相减,得
两式相减,得
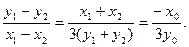
∴k=- . ①
. ①
又∵|AM|=|AN|,
∴AP⊥MN.
∴kAP=-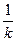 ,即
,即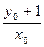 =-
=-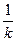 . ②
. ②
联立①②,解得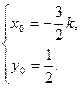
若直线l存在,则P在椭圆内部.
∴ +y02<1,从而得k2<1.
+y02<1,从而得k2<1.
∴-1<k<1且k≠0.
∴满足条件的直线l存在,且k∈(-1,0)∪(0,1).
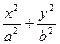 =1,由已知得b=1,
=1,由已知得b=1,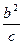 =
=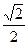 .
.∴c=
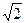 ,a2=3.
,a2=3.∴椭圆方程为
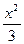 +y2=1.
+y2=1.(2)设M(x1,y1)、N(x2,y2),MN中点P(x0,y0).
∴
 两式相减,得
两式相减,得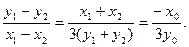
∴k=-
 . ①
. ①又∵|AM|=|AN|,
∴AP⊥MN.
∴kAP=-
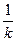 ,即
,即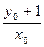 =-
=-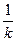 . ②
. ②联立①②,解得
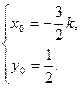
若直线l存在,则P在椭圆内部.
∴
 +y02<1,从而得k2<1.
+y02<1,从而得k2<1.∴-1<k<1且k≠0.
∴满足条件的直线l存在,且k∈(-1,0)∪(0,1).

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
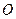 为中心的椭圆的一条准线方程为
为中心的椭圆的一条准线方程为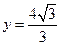 ,离心率
,离心率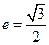 ,
,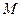 是椭圆上的动点。
是椭圆上的动点。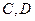 的坐标分别是
的坐标分别是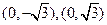 ,求
,求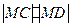 的最大值;
的最大值;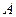 的坐标为
的坐标为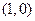 ,
,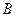 是圆
是圆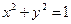 上的点,
上的点,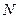 是点
是点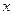 轴上的射影,点
轴上的射影,点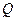 满足条件:
满足条件: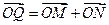 ,
,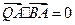 ,求线段
,求线段 的中点
的中点 的轨迹方程。
的轨迹方程。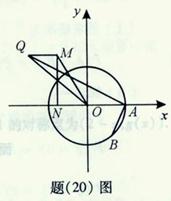
 ,焦点与短轴两端点的连线互相垂直。
,焦点与短轴两端点的连线互相垂直。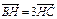 .
.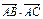 = 0,求以B、C为焦点并且经过点A的椭圆的离心率;
= 0,求以B、C为焦点并且经过点A的椭圆的离心率;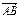 的比为
的比为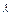 ,A、D同在以B、C为焦点的椭圆上,当 ―5≤
,A、D同在以B、C为焦点的椭圆上,当 ―5≤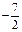 时,求椭圆的离心率e的取值范围.
时,求椭圆的离心率e的取值范围.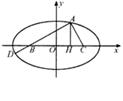
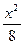 +
+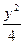 =1上求一点P,使它到定点Q(0,1)的距离最大,则P的坐标是___________.
=1上求一点P,使它到定点Q(0,1)的距离最大,则P的坐标是___________.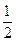 ,求顶点C的轨迹.
,求顶点C的轨迹.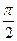 ),方程
),方程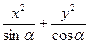 =1表示焦点在x轴上的椭圆,则α的取值范围是( )
=1表示焦点在x轴上的椭圆,则α的取值范围是( )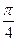 )
)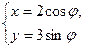 (φ为参数)的离心率为( )
(φ为参数)的离心率为( )