题目内容
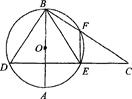
(4—1:几何证明选讲)如图,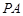 是圆
是圆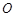 的切线,
的切线,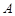 是切点,直线
是切点,直线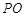 交圆
交圆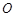 于
于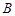 、
、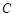 两点,
两点,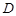 是
是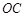 的中点,连结
的中点,连结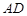 并延长交圆
并延长交圆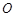 于点
于点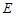 ,若
,若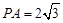 ,∠
,∠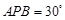 ,则
,则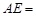 ________.
________.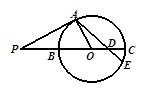
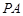 是圆
是圆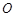 的切线,
的切线,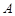 是切点,直线
是切点,直线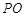 交圆
交圆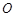 于
于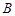 、
、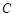 两点,
两点,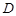 是
是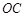 的中点,连结
的中点,连结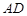 并延长交圆
并延长交圆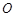 于点
于点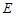 ,若
,若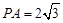 ,∠
,∠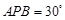 ,则
,则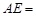 ________.
________.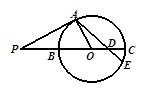

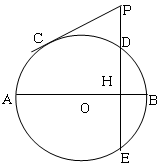
解:连接OA,过O作OF⊥AE,过A作AM⊥PC,如图所示,
∵PA为圆O的切线,
∴∠PAO=90°,又PA= ,∠APB=30°,∴∠AOD=120°,
,∠APB=30°,∴∠AOD=120°,
∴OA=PAtan30°= ×
× 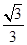 =2,又D为OC中点,故OD=1,
=2,又D为OC中点,故OD=1,
根据余弦定理得:AD2=OA2+OD2-2OA•ODcos∠AOD=4+1+2=7,解得:AD=" 7" ,
∵在Rt△APM中,∠APM=30°,且AP="2" 3 ,
∴AM=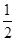 AP=
AP=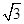 ,
,
故三角形AOD的面积S=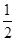 OD•AM=
OD•AM= 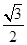 ,则S=
,则S=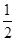 AD•OF=
AD•OF= 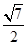 OF=
OF= 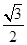 ,
,
∴OF=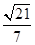 ,
,
在Rt△AOF中,根据勾股定理得:AF2= OA2-OF2 =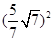 ,
,
则AE=2AF= .
.
故答案为:
∵PA为圆O的切线,
∴∠PAO=90°,又PA=
 ,∠APB=30°,∴∠AOD=120°,
,∠APB=30°,∴∠AOD=120°,∴OA=PAtan30°=
 ×
× 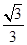 =2,又D为OC中点,故OD=1,
=2,又D为OC中点,故OD=1,根据余弦定理得:AD2=OA2+OD2-2OA•ODcos∠AOD=4+1+2=7,解得:AD=" 7" ,
∵在Rt△APM中,∠APM=30°,且AP="2" 3 ,
∴AM=
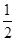 AP=
AP=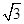 ,
,故三角形AOD的面积S=
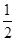 OD•AM=
OD•AM= 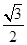 ,则S=
,则S=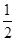 AD•OF=
AD•OF= 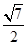 OF=
OF= 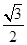 ,
,∴OF=
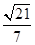 ,
,在Rt△AOF中,根据勾股定理得:AF2= OA2-OF2 =
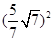 ,
,则AE=2AF=
 .
.故答案为:


练习册系列答案
相关题目
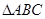 中,
中,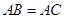 ,
,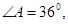 D在AB上,
D在AB上,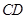 是
是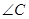 的平分线,则
的平分线,则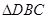 的面积与
的面积与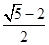
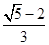
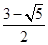
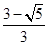
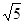 ,求PD的长.
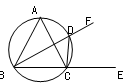
,求PD的长.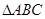 ,过顶点A的圆与边BC切于BC的中点P,与边AB、AC分别交于点M、N,且CN=2BM,点N平分AC.则
,过顶点A的圆与边BC切于BC的中点P,与边AB、AC分别交于点M、N,且CN=2BM,点N平分AC.则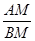 =( )
=( )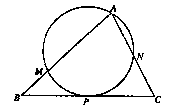
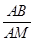 的值.
的值.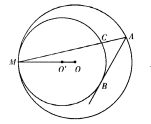
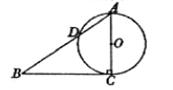
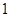 ,C为
,C为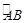 中点.点D,E分别在半径OA,OB上.若CD2+CE2+DE2=
中点.点D,E分别在半径OA,OB上.若CD2+CE2+DE2= ,则OD+OE的取值范围是
,则OD+OE的取值范围是 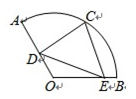
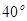 ,则∠DEB___________
,则∠DEB___________