题目内容
如图,在平面直角坐标系xOy中,已知圆C1:(x+1)2+y2=1,圆C2:(x-3)2+(y-4)2=1.
(1)若过点C1(-1,0)的直线l被圆C2截得的弦长为
,求直线l的方程;
(2)设动圆C同时平分圆C1的周长、圆C2的周长.
①证明:动圆圆心C在一条定直线上运动;
②动圆C是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.

(1)若过点C1(-1,0)的直线l被圆C2截得的弦长为
| 6 |
| 5 |
(2)设动圆C同时平分圆C1的周长、圆C2的周长.
①证明:动圆圆心C在一条定直线上运动;
②动圆C是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.

(1)设过点C1(-1,0)的直线l方程:y=k(x+1),化成一般式kx-y+k=0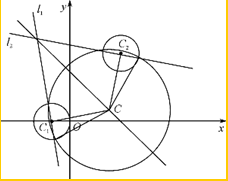
∵直线l被圆C2截得的弦长为
,
∴点C2(3,4)到直线l的距离为d=
=
,
解之得k=
或
由此可得直线l的方程为:4x-3y+4=0或3x-4y+3=0.
(2)①设圆心C(x,y),由题意,得CC1=CC2,
即
=
,
化简整理,得x+y-3=0,
即动圆圆心C在定直线x+y-3=0上运动.
②设圆C过定点,设C(m,3-m),
则动圆C的半径为
=
,
于是动圆C的方程为(x-m)2+(y-3+m)2=1+(m+1)2+(3-m)2,
整理,得x2+y2-6y-2-2m(x-y+1)=0,
由
得
或
所以动圆C经过定点,其坐标为(1-
,2-
),(1+
,2+
).

∵直线l被圆C2截得的弦长为
| 6 |
| 5 |
∴点C2(3,4)到直线l的距离为d=
| |3k-4+k| | ||
|
1-(
|
解之得k=
| 4 |
| 3 |
| 3 |
| 4 |
由此可得直线l的方程为:4x-3y+4=0或3x-4y+3=0.
(2)①设圆心C(x,y),由题意,得CC1=CC2,
即
| (x+1)2+y2 |
| (x-3)2+(y-4)2 |
化简整理,得x+y-3=0,
即动圆圆心C在定直线x+y-3=0上运动.
②设圆C过定点,设C(m,3-m),
则动圆C的半径为
| 1+CC12 |
| 1+(m+1)2+(3-m)2 |
于是动圆C的方程为(x-m)2+(y-3+m)2=1+(m+1)2+(3-m)2,
整理,得x2+y2-6y-2-2m(x-y+1)=0,
由
|
|
|
所以动圆C经过定点,其坐标为(1-
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
| 2 |

练习册系列答案
相关题目
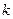 ,直线
,直线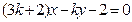 与圆
与圆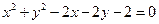 的位置关系是_________
的位置关系是_________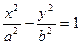 的一个焦点为F1,顶点为A1、A2,P是双曲线上任意一点.则分别以线段PF1、A1A2为直径的两圆一定 ( )
的一个焦点为F1,顶点为A1、A2,P是双曲线上任意一点.则分别以线段PF1、A1A2为直径的两圆一定 ( )