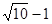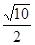题目内容
圆心在直线5x-3y-8=0上的圆与两坐标轴相切,求此圆的方程.
圆的方程为(x-4)2+(y-4)2=16或(x-1)2+(y+1)2=1.
设所求圆的方程为(x-a)2+(y-b)2=r2,
∵圆与两坐标轴相切,
∴圆心满足|a|=|b|,即a-b=0或a+b=0.
又圆心在直线5x-3y-8=0上,
∴5a-3b-8=0.
解方程组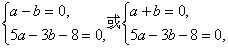
得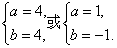
∴圆心坐标为(4,4)或(1,-1),
半径r=|a|=4或r=|a|=1.
∴所求圆的方程为(x-4)2+(y-4)2=16或(x-1)2+(y+1)2=1.
∵圆与两坐标轴相切,
∴圆心满足|a|=|b|,即a-b=0或a+b=0.
又圆心在直线5x-3y-8=0上,
∴5a-3b-8=0.
解方程组
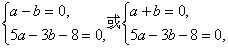
得
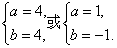
∴圆心坐标为(4,4)或(1,-1),
半径r=|a|=4或r=|a|=1.
∴所求圆的方程为(x-4)2+(y-4)2=16或(x-1)2+(y+1)2=1.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 :
: 与
与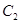 :
:
 相切,则
相切,则 的值为
的值为