题目内容

7．在△ABC中，角A、B、C的对边为a、b、c，则“A=B”成立的必要不充分条件为（　　）
A．cosA=cosBB．sinA=sinBC．bcosA=acosBD．acosA=bcosB

分析 根据充分条件和必要条件的定义进行判断即可．

解答 解：A=B等价于cosA=cosB，
等价于sinA=sinB，排除A、B；
由bcosA=acosB及正弦定理可得sin（A-B）=0，
-π＜A-B＜π，得A=B，排除C；
故选：D．

点评 本题主要考查充分条件和必要条件的判断，比较基础．

练习册系列答案
相关题目
17．在平面直角坐标系xOy中，直线y=-x与圆$\left\{\begin{array}{l}{x=1+cosθ}\\{y=sinθ}\end{array}\right.$（θ为参数）相交，交点在第四象限，则交点的极坐标为$（\sqrt{2}，-\frac{π}{4}）$．
18．下列函数中，在其定义域内既是偶函数又在（-∞，0）上单调递增的函数是（　　）
A．f（x）=x2B．f（x）=-log2|x|C．f（x）=3|x|D．f（x）=sinx
15．执行如图所示的程序框图，输出的结果为（　　）
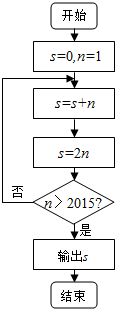
A．210-1B．211-1C．21007-1D．21024-1
2．直角坐标系中，以坐标原点为极点，x轴的非负半轴为极轴，并在两种坐标系中取相同的长度单位．直线l的参数方程是$\left\{\begin{array}{l}{x=1-\frac{\sqrt{2}}{2}t}\\{y=-4+\frac{\sqrt{2}}{2}t}\end{array}\right.$（t为参数），曲线c的极坐标方程为ρ2-10ρcosθ+9=0，点P是直线l上的点，过点P的直线与曲线c相切于点M，则|PM|最小值为4．
12．在极坐标系中，曲线C：ρ=2sinθ，A、B为曲线C的两点，以极点为原点，极轴为x轴非负半轴的直角坐标中，曲线E：$\left\{{\begin{array}{l}{x=4t+2}\\{y=-3t-3}\end{array}}\right.$上一点P，则∠APB的最大值为（　　）
A．$\frac{π}{4}$B．$\frac{π}{3}$C．$\frac{π}{2}$D．$\frac{2π}{3}$
19．已知抛物线y=ax2+bx+c（a≠0）的对称轴在y轴的左侧，其中a、b、c∈{-3，-2，-1，0，1，2，3}，在这些抛物线中，记随机变量X=|a-b|，则X的均值EX为（　　）
A．$\frac{8}{9}$B．$\frac{3}{5}$C．$\frac{2}{5}$D．$\frac{1}{3}$
10．函数f（x）=$\frac{1}{3}$x3-3x2+5x+9的极大值点为x=1．
11．已知函数f（x）=alnx+$\frac{1}{x}$（a≠0）
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）若存在两条直线y=ax+b1，y=ax+b2（b1≠b2）都是曲线y=f（x）的切线．求实数a的取值范围；
（Ⅲ）若|x|f（x）≤0}⊆（0，1），求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网