题目内容
12.在极坐标系中,曲线C:ρ=2sinθ,A、B为曲线C的两点,以极点为原点,极轴为x轴非负半轴的直角坐标中,曲线E:$\left\{{\begin{array}{l}{x=4t+2}\\{y=-3t-3}\end{array}}\right.$上一点P,则∠APB的最大值为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
分析 由曲线C:ρ=2sinθ,化为ρ2=2ρsinθ,利用$\left\{\begin{array}{l}{{ρ}^{2}={x}^{2}+{y}^{2}}\\{y=ρsinθ}\end{array}\right.$可得直角坐标方程.曲线E:$\left\{{\begin{array}{l}{x=4t+2}\\{y=-3t-3}\end{array}}\right.$,消去参数t可得普通方程.当∠APB取最大值时,PA、PB与圆C相切,且PC最短即PC⊥l,利用直角三角形的边角关系即可得出.
解答 解:由曲线C:ρ=2sinθ,化为ρ2=2ρsinθ,
∴x2+y2=2y,配方为x2+(y-1)2=1.
曲线E:$\left\{{\begin{array}{l}{x=4t+2}\\{y=-3t-3}\end{array}}\right.$,消去参数t可得普通方程为3x+4y+6=0.
当∠APB取最大值时,PA、PB与圆C相切,且PC最短即PC⊥l,
此时在Rt△PAC中,$sin∠APC=\frac{1}{2}$,故$∠APC=\frac{π}{6}$,∠APB为$\frac{π}{3}$.
故选:B.
点评 本题考查了把参数方程化为普通方程、极坐标方程化为直角坐标方程、圆的切线的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
7.在△ABC中,角A、B、C的对边为a、b、c,则“A=B”成立的必要不充分条件为( )
| A. | cosA=cosB | B. | sinA=sinB | C. | bcosA=acosB | D. | acosA=bcosB |
16.函数f(x)=(x-3)ex的单调递增区间是( )
| A. | (2,+∞) | B. | (0,3) | C. | (1,4) | D. | (-∞,2) |
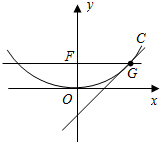 设p>0,抛物线方程为C:x2=2px.如图所示,过焦点F作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过点(0,-1).
设p>0,抛物线方程为C:x2=2px.如图所示,过焦点F作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过点(0,-1).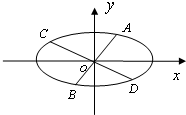 椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条直线段,称为该直径的共轭直径.已知椭圆的方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1
椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条直线段,称为该直径的共轭直径.已知椭圆的方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1