题目内容
17.在平面直角坐标系xOy中,直线y=-x与圆$\left\{\begin{array}{l}{x=1+cosθ}\\{y=sinθ}\end{array}\right.$(θ为参数)相交,交点在第四象限,则交点的极坐标为$(\sqrt{2},-\frac{π}{4})$.分析 化圆的参数方程为普通方程,联立直线方程和圆的方程,求出在第四象限的交点坐标,化为极坐标得答案.
解答 解:由$\left\{\begin{array}{l}{x=1+cosθ}\\{y=sinθ}\end{array}\right.$,得(x-1)2+y2=1.
联立$\left\{\begin{array}{l}{y=-x}\\{(x-1)^{2}+{y}^{2}=1}\end{array}\right.$,解得直线y=-x与圆(x-1)2+y2=1在第四象限的交点为(1,-1),
转化为极坐标为$(\sqrt{2},-\frac{π}{4})$.
故答案为:$(\sqrt{2},-\frac{π}{4})$.
点评 本题考查参数方程化普通方程,考查方程组的解法,训练了直角坐标化极坐标,是基础题.

练习册系列答案
相关题目
7.已知直线l过点(1,0),且与直线x-y+1=0垂直,若直线l与圆C:x2+y2+2y-3=0相交于A、B两点,则△ABC的面积为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
8.已知抛物线y2=4x的准线与双曲线$\frac{x^2}{3}-\frac{y^2}{b^2}=1$的一条准线重合,则这条抛物线y2=4x与双曲线$\frac{x^2}{3}-\frac{y^2}{b^2}=1$的交点P到抛物线焦点的距离为( )
| A. | $\sqrt{21}$ | B. | 21 | C. | 6 | D. | 4 |
12.抛物线y=$\frac{1}{8}$x2上到焦点的距离等于10的点的坐标为( )
| A. | (-8,8) | B. | (8,8) | C. | (-8,-8)或(8,-8) | D. | (-8,8)或(8,8) |
7.在△ABC中,角A、B、C的对边为a、b、c,则“A=B”成立的必要不充分条件为( )
| A. | cosA=cosB | B. | sinA=sinB | C. | bcosA=acosB | D. | acosA=bcosB |
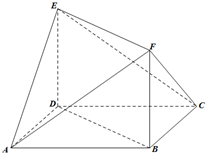 如图,多面体ABCDEF中,DE⊥平面ABCD,底面ABCD是菱形,AB=2,
如图,多面体ABCDEF中,DE⊥平面ABCD,底面ABCD是菱形,AB=2,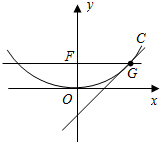 设p>0,抛物线方程为C:x2=2px.如图所示,过焦点F作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过点(0,-1).
设p>0,抛物线方程为C:x2=2px.如图所示,过焦点F作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过点(0,-1).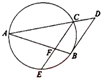 如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于D.过点C作BD的平行线与圆交于点E,与AB相交于点F,AF=4,FB=1,EF=2,则线段AC的长为4.
如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于D.过点C作BD的平行线与圆交于点E,与AB相交于点F,AF=4,FB=1,EF=2,则线段AC的长为4.