题目内容
14.已知幂函数f(x)的图象经过(3,27),则f(2)=8.分析 设幂函数f(x)=xa,把点(3,27)代入,得3a=27,解得a=3.故f(x)=x3,再将x=2代入可得答案.
解答 解:设幂函数f(x)=xa,
把点(3,27)代入,得
3a=27,
解得a=3.
∴f(x)=x3,
∴f(2)=23=8,
故答案为:8
点评 本题考查幂函数的单调性、奇偶性及其应用,是基础题.解题时要认真审题,注意待定系数法的合理运用.

练习册系列答案
相关题目
4.函数f(x)=sinx-2x在区间[0,2π]上的最小值是( )
| A. | -4π | B. | 0 | C. | -2π | D. | 1-π |
2.函数f(x)=$\sqrt{3}$x+2cosx在区间[0,$\frac{π}{2}$]上的最大值是( )
| A. | 2 | B. | $\frac{\sqrt{3}π}{2}$ | C. | $\frac{\sqrt{3}π+3}{3}$ | D. | 1 |
9.如图程序图输出的结果是( )
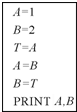
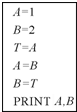
| A. | 2,1 | B. | 2,2 | C. | 1,2 | D. | 1,1 |
19.已知过点(-2,3)可以作圆(x-a)2+(y-2)2=9的两条切线,则a的范围是( )
| A. | (-∞,-3)∪(3,+∞) | B. | $(-∞,-2-2\sqrt{2})∪(-2+2\sqrt{2},+∞)$ | ||
| C. | (-3,3) | D. | $(-2-2\sqrt{2},-2+2\sqrt{2})$ |
6.下列函数中,在其定义域内既是奇函数又是减函数的是( )
| A. | y=($\frac{1}{2}$)x,x∈R | B. | y=$\frac{1}{x-1}$,x≠1 | C. | y=x+sinx,x∈R | D. | y=-x3-x,x∈R |
 如图所示,已知半圆的直径AB=6cm,CD是半圆上长为2cm的弦,问:当弦CD在半圆上滑动时,AC和BD延长线的夹角是定值吗?若是,试求出这个定角的正弦值;若不是,请说明理由.
如图所示,已知半圆的直径AB=6cm,CD是半圆上长为2cm的弦,问:当弦CD在半圆上滑动时,AC和BD延长线的夹角是定值吗?若是,试求出这个定角的正弦值;若不是,请说明理由.