题目内容
9．如图程序图输出的结果是（ ）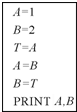
| A． | 2，1 | B． | 2，2 | C． | 1，2 | D． | 1，1 |
分析 根据已知中的程序框图，逐步分析执行完相应语句后的变量的值，可得答案．
解答 解：执行A=1，B=2后：A=1，B=2；
执行T=A后：A=1，B=2，T=1；
执行A=B后：A=2，B=2，T=1；
执行B=T后：A=2，B=1，T=1；
执行PRINT A，B后，输出的结果为2，1，
故选：A
点评 本题考查的知识点是程序框图，顺序结构，难度不大，属于基础题．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
相关题目
19．函数y=x3-3x2-9x（-2＜x＜2）有（ ）
| A． | 极大值5，无极小值 | B． | 极小值-27，无极大值 | ||
| C． | 极大值5，极小值-27 | D． | 极大值5，极小值-11 |
17．在△ABC中，若tan A•tan B＜1，则△ABC的形状是（ ）
| A． | 锐角三角形 | |
| B． | 直角三角形 | |
| C． | 钝角三角形 | |
| D． | 可能是锐角三角形，也可能是钝角三角形 |
4．一商场对每天进店人数和商品销售件数进行了统计对比，得到如下表格：
参考数据：$\sum_{i=1}^{7}$xiyi=3245，$\overline{x}$=25，$\overline{y}$≈15，$\sum_{i=1}^{7}$xi2=5075．
参考公式：b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x\overline{y}}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，a=$\overline{y}$-b$\overline{x}$
（1）由散点图可知进店人数和商品销售件数成线性相关关系，设回归方程为$\widehat{y}$=bx+a，求该回归方程（b保留到小数点后两位）；
（2）预测进店80人时，商品销售的件数（结果保留整数）．
| 人数xi（人） | 10 | 15 | 20 | 25 | 30 | 35 | 40 |
| 件数yi（件） | 4 | 7 | 12 | 12 | 20 | 23 | 27 |
参考公式：b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x\overline{y}}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，a=$\overline{y}$-b$\overline{x}$
（1）由散点图可知进店人数和商品销售件数成线性相关关系，设回归方程为$\widehat{y}$=bx+a，求该回归方程（b保留到小数点后两位）；
（2）预测进店80人时，商品销售的件数（结果保留整数）．
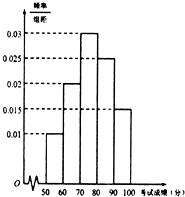某市为了了解本地高中学生的汉字书写水平，在全市范围内随机抽取了近千名学生参加汉字听写考试，将所得数据整理后，绘制出频率分布直方图如图所示，其中样本数据分组区间为[50，60），[60，70），[70，80），[80，90），[90，100]．