题目内容
3.已知a1=1,an+1>an,且(an+1-an)2-2(an+1+an)+1=0,计算a2,a3,然后猜想an.分析 由题设条件知(a2-1)2-2(a2+1)+1=0,所以a2=4.由(a3-4)2-2(a3+4)+1=0,知a3=9由此猜想an=n2.
解答 解:∵a1=1,an+1>an,且(an+1-an)2-2(an+1+an)+1=0,
∴(a2-1)2-2(a2+1)+1=0,
整理得a22-4a2=0,
∴a2=4或a2=0(舍).
(a3-4)2-2(a3+4)+1=0,
整理,得a32-10a3+9=0,
∴a3=9或a3=1(舍).
由此猜想an=n2.
故答案为:n2.
点评 本题考查数列的性质和应用,解题时要注意递推公式的应用,寻代各项和规律,合理地进行猜想.

练习册系列答案
相关题目
13.已知2弧度的圆心角所对的弦长为4,那么这个圆心角所对的弧长为( )
| A. | 4 | B. | sin 2 | C. | $\frac{4}{sin1}$ | D. | 4sin 1 |
12.设a=$\int_{1}^{2}{(3{x^2}-2x)dx}$,则二项式${(a{x^2}-\frac{1}{x})^6}$的展开式中的常数项为( )
| A. | 120 | B. | -120 | C. | -240 | D. | 240 |
13.把一枚硬币任意抛掷三次,事件A表示“至少一次出现反面”,事件B表示“恰有一次出现正面”,则P(B|A)值等于( )
| A. | $\frac{21}{64}$ | B. | $\frac{7}{64}$ | C. | $\frac{1}{7}$ | D. | $\frac{3}{7}$ |
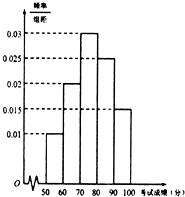 某市为了了解本地高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示,其中样本数据分组区间为[50,60),[60,70),[70,80),[80,90),[90,100].
某市为了了解本地高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示,其中样本数据分组区间为[50,60),[60,70),[70,80),[80,90),[90,100].