题目内容
19．已知过点（-2，3）可以作圆（x-a）2+（y-2）2=9的两条切线，则a的范围是（ ）| A． | （-∞，-3）∪（3，+∞） | B． | $（-∞，-2-2\sqrt{2}）∪（-2+2\sqrt{2}，+∞）$ | ||
| C． | （-3，3） | D． | $（-2-2\sqrt{2}，-2+2\sqrt{2}）$ |
分析 由题意得（-2，3）在圆外，可得（-2-a）2+（3-2）2＞9，解不等式组求出a取值范围．
解答 解：由题意（-2，3）在圆外，∴（-2-a）2+（3-2）2＞9，
解得a＜-2-2$\sqrt{2}$或a＞-2+2$\sqrt{2}$，
故选：B．
点评 本题考查点与圆的位置关系，利用圆的标准方程求圆心和半径，两点间的距离公式以及一元二次不等式的解法．
练习册系列答案
相关题目
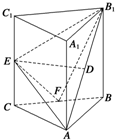三棱柱ABC-A1B1C1中，侧棱AA1⊥平面ABC，△ABC为等腰直角三角形，∠BAC=90°且AB=AA1，D，E，F分别是B1A，CC1，BC的中点．
4．已知集合A={0，1，2}，集合B={-1，0，1}，则集合A∩B=（ ）
| A． | {-1，0，1，2} | B． | {0，1} | C． | {-1，6} | D． | ∅ |