题目内容
5. 如图所示,已知半圆的直径AB=6cm,CD是半圆上长为2cm的弦,问:当弦CD在半圆上滑动时,AC和BD延长线的夹角是定值吗?若是,试求出这个定角的正弦值;若不是,请说明理由.
如图所示,已知半圆的直径AB=6cm,CD是半圆上长为2cm的弦,问:当弦CD在半圆上滑动时,AC和BD延长线的夹角是定值吗?若是,试求出这个定角的正弦值;若不是,请说明理由.
分析 连接BC,利用圆周角定理可知∠PBC为定值,则可知∠P为定值,又可证明△PCD∽△PBA,可求得PC和PB的比值,在Rt△PCB中,可求得∠P的正弦值.
解答 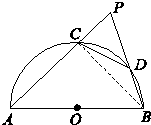 解:当弦CD在半圆上滑动时,AC和BD延长线的夹角是定值.
解:当弦CD在半圆上滑动时,AC和BD延长线的夹角是定值.
理由如下,如图所示,连接BC.
∵CD为定长,虽CD滑动,但的度数不变,
∴∠PBC为定值,
∴∠P=∠ACB-∠PBC=90°-∠PBC,为定值.
∵∠PCD=∠PBA,
∴△PCD∽△PBA,
∴$\frac{PC}{PB}$=$\frac{CD}{BA}$=$\frac{2}{6}$=$\frac{1}{3}$.
在Rt△PBC中,cos∠P=$\frac{PC}{PB}$=$\frac{1}{3}$,
∴sin∠P=$\sqrt{1-{{(\frac{1}{3})}^2}}=\frac{{2\sqrt{2}}}{3}$.
点评 本题主要考查相似三角形的判定和性质及圆周角定理和三角函数的定义,掌握相似三角形的对应边成比例,找到PC和BC的关系是解题关键.

练习册系列答案
相关题目
13.已知2弧度的圆心角所对的弦长为4,那么这个圆心角所对的弧长为( )
| A. | 4 | B. | sin 2 | C. | $\frac{4}{sin1}$ | D. | 4sin 1 |
17.在△ABC中,若tan A•tan B<1,则△ABC的形状是( )
| A. | 锐角三角形 | |
| B. | 直角三角形 | |
| C. | 钝角三角形 | |
| D. | 可能是锐角三角形,也可能是钝角三角形 |