题目内容
2.函数f(x)=$\sqrt{3}$x+2cosx在区间[0,$\frac{π}{2}$]上的最大值是( )| A. | 2 | B. | $\frac{\sqrt{3}π}{2}$ | C. | $\frac{\sqrt{3}π+3}{3}$ | D. | 1 |
分析 利用导数研究函数的单调性,利用单调性求函数的最大值为f($\frac{π}{3}$),计算求的结果.
解答 解:∵函数f(x)=$\sqrt{3}$x+2cosx,∴f′(x)=$\sqrt{3}$-2sinx
f′(x)=$\sqrt{3}$-2sinx 在区间[0,$\frac{π}{3}$)上大于零,在($\frac{π}{3}$,$\frac{π}{2}$]上小于零,
故函数f(x)在区间[0,$\frac{π}{3}$)上单调递增,在($\frac{π}{3}$,$\frac{π}{2}$]上单调递减,
故函数f(x)=$\sqrt{3}$x+2cosx在区间[0,$\frac{π}{2}$]上的最大值是f($\frac{π}{3}$)=$\frac{\sqrt{3}}{3}π$+1,
故选:C.
点评 本题主要考查利用导数研究函数的单调性,利用单调性求函数的最值,属于中档题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
12.设x,y∈R,若x-|y|>0,则下列不等式中正确的是( )
| A. | $\frac{1}{x}$<$\frac{1}{y}$ | B. | $\frac{1}{x}$>$\frac{1}{y}$ | C. | x2<y2 | D. | x2>y2 |
13.已知2弧度的圆心角所对的弦长为4,那么这个圆心角所对的弧长为( )
| A. | 4 | B. | sin 2 | C. | $\frac{4}{sin1}$ | D. | 4sin 1 |
17.在△ABC中,若tan A•tan B<1,则△ABC的形状是( )
| A. | 锐角三角形 | |
| B. | 直角三角形 | |
| C. | 钝角三角形 | |
| D. | 可能是锐角三角形,也可能是钝角三角形 |
12.设a=$\int_{1}^{2}{(3{x^2}-2x)dx}$,则二项式${(a{x^2}-\frac{1}{x})^6}$的展开式中的常数项为( )
| A. | 120 | B. | -120 | C. | -240 | D. | 240 |
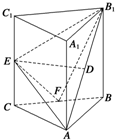 三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°且AB=AA1,D,E,F分别是B1A,CC1,BC的中点.
三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°且AB=AA1,D,E,F分别是B1A,CC1,BC的中点.