题目内容
(本题满分12分)
在直角坐标系 中,动点
中,动点 到两圆
到两圆 的圆心
的圆心 和
和 的距离的和等于
的距离的和等于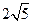 .
.
(Ⅰ) 求动点 的轨迹方程;
的轨迹方程;
(Ⅱ) 以动点 的轨迹与
的轨迹与 轴正半轴的交点C为直角顶点作此轨迹的内接等腰直角三角形ABC,试问:这样的等腰直角三角形是否存在?若存在,有几个?若不存在,请说明理由.
轴正半轴的交点C为直角顶点作此轨迹的内接等腰直角三角形ABC,试问:这样的等腰直角三角形是否存在?若存在,有几个?若不存在,请说明理由.
在直角坐标系
 中,动点
中,动点 到两圆
到两圆 的圆心
的圆心 和
和 的距离的和等于
的距离的和等于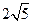 .
.(Ⅰ) 求动点
 的轨迹方程;
的轨迹方程;(Ⅱ) 以动点
 的轨迹与
的轨迹与 轴正半轴的交点C为直角顶点作此轨迹的内接等腰直角三角形ABC,试问:这样的等腰直角三角形是否存在?若存在,有几个?若不存在,请说明理由.
轴正半轴的交点C为直角顶点作此轨迹的内接等腰直角三角形ABC,试问:这样的等腰直角三角形是否存在?若存在,有几个?若不存在,请说明理由.解:(Ⅰ)两圆的圆心坐标分别为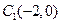 、
、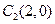 ,根据椭圆的定义可知,动点
,根据椭圆的定义可知,动点 的轨迹为以
的轨迹为以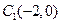 、
、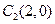 为焦点,长轴长等于
为焦点,长轴长等于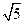 的椭圆.
的椭圆.
由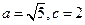 得
得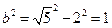 ,所以,动点
,所以,动点 的轨迹方程
的轨迹方程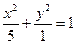
(Ⅱ)由(Ⅰ)得C点的坐标为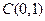
不妨设A、B两点分居于y轴的左、右两侧,设CA的斜率为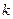 ,
,
则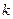 >0,CA所在直线的方程为
>0,CA所在直线的方程为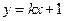 .
.
代入椭圆方程并整理得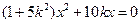 .
.
∴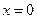 或
或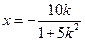 .∴A点的坐标为
.∴A点的坐标为 .
.
∴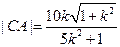 . 同理,
. 同理,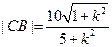 .
.
由|CA|=|CB|得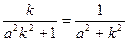 ,
,
∴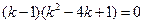 解得
解得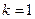 或
或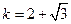 或
或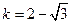
∴符合题意的等腰直角三角形一定存在,且有3个.
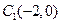 、
、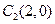 ,根据椭圆的定义可知,动点
,根据椭圆的定义可知,动点 的轨迹为以
的轨迹为以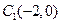 、
、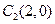 为焦点,长轴长等于
为焦点,长轴长等于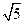 的椭圆.
的椭圆.由
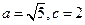 得
得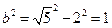 ,所以,动点
,所以,动点 的轨迹方程
的轨迹方程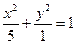
(Ⅱ)由(Ⅰ)得C点的坐标为
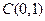
不妨设A、B两点分居于y轴的左、右两侧,设CA的斜率为
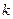 ,
,则
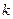 >0,CA所在直线的方程为
>0,CA所在直线的方程为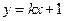 .
.代入椭圆方程并整理得
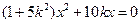 .
.∴
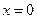 或
或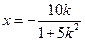 .∴A点的坐标为
.∴A点的坐标为 .
.∴
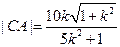 . 同理,
. 同理,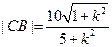 .
.由|CA|=|CB|得
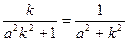 ,
,∴
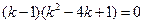 解得
解得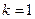 或
或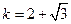 或
或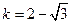
∴符合题意的等腰直角三角形一定存在,且有3个.
略

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
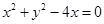 的圆心坐标和半径分别为
的圆心坐标和半径分别为



 满足
满足 ,过点P的直线
,过点P的直线 与圆
与圆 相交于A、B 两点,则
相交于A、B 两点,则 的最小值是( )
的最小值是( ) B.4 C.
B.4 C. D.3
D.3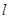 与圆
与圆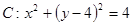 有公共点, 则直线
有公共点, 则直线
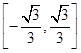
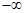 ,
,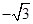 )∪[
)∪[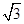 ,+
,+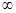 ]
]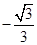 )∪[
)∪[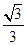 ,+
,+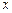 轴相切,圆心在直线
轴相切,圆心在直线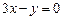 上,且被直线
上,且被直线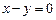 截下的弦长为
截下的弦长为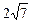 的圆的方程。
的圆的方程。 ≤λ≤1
≤λ≤1  <
<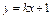 与曲线
与曲线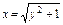 有两个不同的交点,则k的取值范围是_____
有两个不同的交点,则k的取值范围是_____ 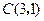 为圆心,且与
为圆心,且与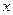 轴相切的圆的方程是 .
轴相切的圆的方程是 .