题目内容
已知圆C与圆(x-1)2+y2=1关于直线y=-x对称,则圆C的方程为( )
| A.(x+1)2+y2=1 | B.x2+y2=1 |
| C.x2+(y+1)2=1 | D.x2+(y-1)2=1 |
C
分析:设出圆C上的任意一点M坐标,求出关于直线y=-x对称的点的坐标,代入已知圆的方程化简即可.
解:由圆C上的任意一点M(x,y)关于y=-x的对称点为(-y,-x),(-y,-x)在圆(x-1)2+y2=1上,
代入化简即得x2+(y+1)2=1.
故选C.
点评:本题考查关于直线对称的圆的方程,考查计算能力,是基础题
解:由圆C上的任意一点M(x,y)关于y=-x的对称点为(-y,-x),(-y,-x)在圆(x-1)2+y2=1上,
代入化简即得x2+(y+1)2=1.
故选C.
点评:本题考查关于直线对称的圆的方程,考查计算能力,是基础题

练习册系列答案
相关题目
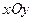 中,已知直线
中,已知直线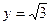 被圆[
被圆[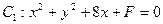 截得的弦长为
截得的弦长为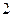
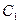 的方程
的方程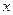 轴相交于
轴相交于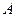 ,
,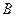 两点,点
两点,点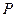 为圆
为圆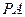 ,
,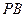 交
交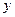 轴于
轴于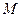 ,
,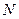 两点.当点
两点.当点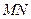 为直径的圆
为直径的圆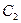 是否经过圆
是否经过圆 中,动点
中,动点 到两圆
到两圆 的圆心
的圆心 和
和 的距离的和等于
的距离的和等于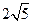 .
. 轴正半轴的交点C为直角顶点作此轨迹的内接等腰直角三角形ABC,试问:这样的等腰直角三角形是否存在?若存在,有几个?若不存在,请说明理由.
轴正半轴的交点C为直角顶点作此轨迹的内接等腰直角三角形ABC,试问:这样的等腰直角三角形是否存在?若存在,有几个?若不存在,请说明理由.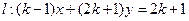 和圆
和圆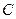 :
: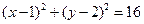 .
.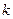 取何值,直线
取何值,直线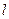 与圆
与圆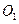 与⊙
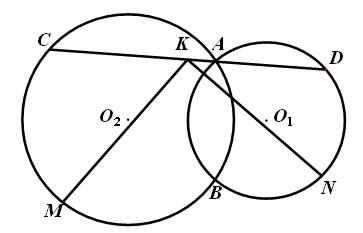
与⊙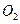 相交于点A和B,经过A作直线与⊙
相交于点A和B,经过A作直线与⊙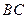 的中点为M,弧
的中点为M,弧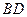 的中点为N,线段CD的中点为K. 求证:
的中点为N,线段CD的中点为K. 求证: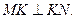
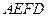 的两条对角线相交于点
的两条对角线相交于点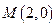 ,
,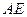 边所在直线的方程为:
边所在直线的方程为: 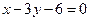 ,点
,点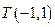 在
在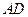 边所在直线上.
边所在直线上.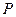 的方程。
的方程。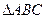 是圆
是圆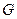 的坐标是
的坐标是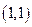 ,求直线
,求直线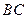 的方程 .
的方程 .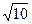 ,求圆C的方程
,求圆C的方程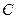 经过不同的三点P(k,0)、Q(2,0)、R(0,1),已知圆
经过不同的三点P(k,0)、Q(2,0)、R(0,1),已知圆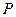 点的切线斜率为1,试求圆
点的切线斜率为1,试求圆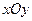 中,已知圆
中,已知圆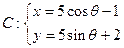 (
(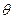 为参数)和直线
为参数)和直线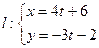 (
(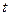 为参数),则圆C的普通方程为 ,直线
为参数),则圆C的普通方程为 ,直线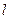 与圆C的位置关系是
与圆C的位置关系是