题目内容
(本小题满分10分)求与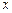 轴相切,圆心在直线
轴相切,圆心在直线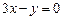 上,且被直线
上,且被直线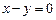 截下的弦长为
截下的弦长为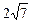 的圆的方程。
的圆的方程。
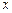 轴相切,圆心在直线
轴相切,圆心在直线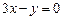 上,且被直线
上,且被直线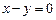 截下的弦长为
截下的弦长为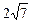 的圆的方程。
的圆的方程。解:由于圆心在直线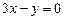 上,故可设圆心为
上,故可设圆心为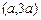
由题意可知半径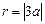 ,且圆心到直线的距离
,且圆心到直线的距离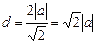
∴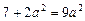 ,解得
,解得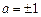
当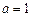 时,
时,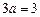 ,
,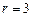 ;
;
当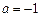 时,
时,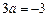 ,
,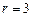
故所求圆的方程为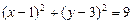 或
或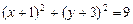
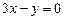 上,故可设圆心为
上,故可设圆心为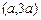
由题意可知半径
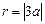 ,且圆心到直线的距离
,且圆心到直线的距离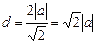
∴
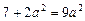 ,解得
,解得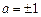
当
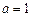 时,
时,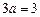 ,
,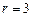 ;
;当
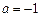 时,
时,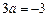 ,
,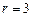
故所求圆的方程为
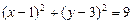 或
或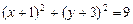
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, 且圆心在直线
且圆心在直线 上圆的方程是( )
上圆的方程是( )


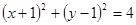
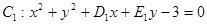 和
和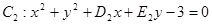 都过点E(3,4),则经过两点
都过点E(3,4),则经过两点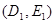 、
、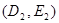 的直线方程为
的直线方程为 中,动点
中,动点 到两圆
到两圆 的圆心
的圆心 和
和 的距离的和等于
的距离的和等于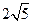 .
. 轴正半轴的交点C为直角顶点作此轨迹的内接等腰直角三角形ABC,试问:这样的等腰直角三角形是否存在?若存在,有几个?若不存在,请说明理由.
轴正半轴的交点C为直角顶点作此轨迹的内接等腰直角三角形ABC,试问:这样的等腰直角三角形是否存在?若存在,有几个?若不存在,请说明理由.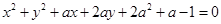 表示圆,则
表示圆,则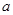 的取值范围是 ( )
的取值范围是 ( ) 或
或



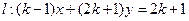 和圆
和圆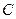 :
: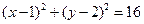 .
.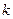 取何值,直线
取何值,直线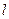 与圆
与圆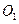 与⊙
与⊙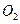 相交于点A和B,经过A作直线与⊙
相交于点A和B,经过A作直线与⊙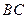 的中点为M,弧
的中点为M,弧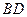 的中点为N,线段CD的中点为K. 求证:
的中点为N,线段CD的中点为K. 求证: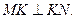
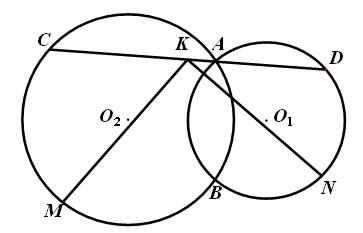
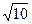 ,求圆C的方程
,求圆C的方程