题目内容

20．函数f（x）=2x3-4x 的单调递减区间是（　　）
A．（-$\sqrt{6}$，$\sqrt{6}$）B．（-$\frac{\sqrt{2}}{3}$，$\frac{\sqrt{2}}{3}$）C．（-$\frac{\sqrt{6}}{3}$，$\frac{\sqrt{6}}{3}$）D．（-$\frac{\sqrt{3}}{3}$，$\frac{\sqrt{3}}{3}$）

分析 求出函数的导函数，令导函数小于0，求出x的范围，写成区间的形式即为函数的单调递减区间

解答 解：因为f′（x）=6x2-4=6（x+$\frac{\sqrt{6}}{3}$）（x-$\frac{\sqrt{6}}{3}$），
令f′（x）＜0，解得-$\frac{\sqrt{6}}{3}$＜x＜$\frac{\sqrt{6}}{3}$
所以函数f（x）=2x3-4x 的单调递减区间（-$\frac{\sqrt{6}}{3}$，$\frac{\sqrt{6}}{3}$）．
故选：C．

点评 本题考查根据导函数的符号与函数单调性的关系，求函数的单调区间，属于基础题．

练习册系列答案
相关题目
10．f（x）是R上的可导函数，且f（x）+xf′（x）＞0对x∈R恒成立，则下列恒成立的是（　　）
A．f（x）＞0B．f（x）＜0C．f（x）＞xD．f（x）＜x
11．已知方程3x-a=x+1的解是正数，求a的取值范围．
8．已知函数f（x）=cos$（2ωx+\frac{π}{3}）$+$\frac{1}{2}$ （ω＞0）的最小正周期是π．
（1）求函数f（x）的单调递增区间和对称中心；
（2）若A为钝角三角形ABC的最小内角，求f（A）的取值范围．
15．已知复数z=$\frac{（1+i）2+3（1-i）}{2+i}$则z的共轭复数$\overline{z}$=1+i．
5．已知数列{an}是各项均为正数有穷数列，数列{bn}满足kbk=a1+a2+…+ak（k=1，2，…，n）
（1）若数列{bn}的通项公式bn=n，求数列{an}的通项公式；
（2）①若数列{an}为递增数列，试判断数列{bn}是否为递增数列？如果是，请加以证明；如果不是，说明理由；
②若数列{bn}为递增数列，试判断数列{an}是否为递增数列？如果是，请加以证明；如果不是，说明理由；
（3）设数列{Cn}、{Dn}满足：Cn=（a1-b1）2+（a2-b2）2+…+（an-bn）2，Dn=（a1-bn）2+（a2-bn）2+…+（an-bn）2，求证：Cn≤Dn．
12．给出下面三个命题：
①已知随机变量ξ服从正态分布N（0，σ2），且P（-2≤ξ≤2）=0.9，则P（ξ＞2）=0.05；
②某学生在最近的15次数学测验中有5次不及格．按照这个成绩，他在接下来的6次测验中，恰好前4次及格的概率为（$\frac{2}{3}$）4（$\frac{1}{3}$）2；
③假定生男孩、生女孩是等可能的．在一个有两个孩子的家庭中，已知有一个是女孩，则另一个孩子也是女孩的概率是$\frac{1}{4}$．
则正确的序号为（　　）
A．①②B．①③C．①D．②
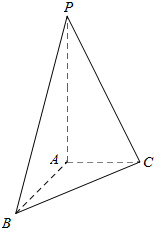9．如图，在三棱锥P-ABC中，PA丄平面ABC，AC丄AB，PA=AB=2，AC=1．
（Ⅰ） 证明：PC丄AB；
（Ⅱ）求二面角A-PC-B的正弦值；
（Ⅲ） 求三棱锥P-ABC外接球的体积．
10．已知函数f（x）=asinx+cosx的图象经过点$（\frac{π}{2}，-1）$．
（1）求函数f（x）的最小正周期与单调递增区间．
（2）若$θ∈（{0，\frac{π}{2}}）$，且f（θ）=$\frac{1}{2}$，求sin2θ的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网