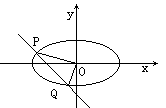题目内容
(本小题满分14分)
已知椭圆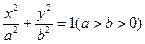 的左右焦点分别为
的左右焦点分别为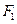 、
、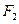 ,离心率
,离心率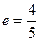 ,直线
,直线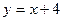 经过椭圆的左焦点
经过椭圆的左焦点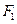 .
.
(1)求该椭圆的方程;
(2)若该椭圆上有一点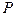 满足:
满足: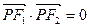 ,求
,求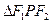 的面积.
的面积.
已知椭圆
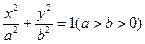 的左右焦点分别为
的左右焦点分别为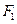 、
、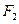 ,离心率
,离心率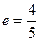 ,直线
,直线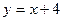 经过椭圆的左焦点
经过椭圆的左焦点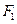 .
.(1)求该椭圆的方程;
(2)若该椭圆上有一点
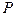 满足:
满足: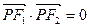 ,求
,求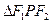 的面积.
的面积.(1)

(2)9
解:(1)直线
 与
与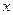 的交点的坐标为
的交点的坐标为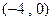 , ……………1分
, ……………1分则
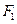 的坐标为
的坐标为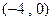 ,
, . …………… 2分
. …………… 2分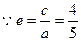 ,
,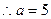 ,
, . ……………5分
. ……………5分则椭圆的方程为
 . ……………6分
. ……………6分(2)由
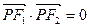 得:
得: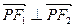 ,所以
,所以 , ……………8分
, ……………8分所以
 是直角三角形, ……………9分
是直角三角形, ……………9分 . ……………10分
. ……………10分又
 ,
,  ……………12分
……………12分

 . ……………14分
. ……………14分
练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
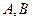 是椭圆
是椭圆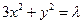 上的两点,点
上的两点,点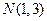 是线段
是线段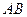 的中点,线段
的中点,线段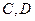 两点.
两点.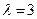 时,过点P(0,1)且倾斜角为
时,过点P(0,1)且倾斜角为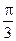 的直线与椭圆相交于E、F两点,求
的直线与椭圆相交于E、F两点,求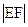 长;
长;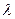 的取值范围,并求直线CD的方程.
的取值范围,并求直线CD的方程.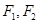 是椭圆
是椭圆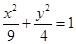 的两个焦点,
的两个焦点,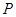 是椭圆上的点,且
是椭圆上的点,且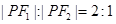 ,则
,则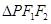 的面积为
的面积为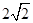
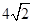
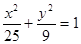 上一点M到焦点
上一点M到焦点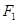 的距离为2,
的距离为2,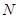 是
是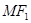 的中点,则
的中点,则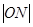 等于( )
等于( )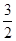
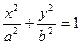 (
(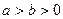 )的两个焦点分别为
)的两个焦点分别为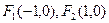 ,点P在椭圆上,且满足
,点P在椭圆上,且满足 ,
,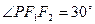 ,直线
,直线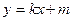 与圆
与圆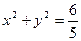 相切,与椭圆相交于A,B两点.
相切,与椭圆相交于A,B两点.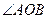 为定值(O为坐标原点)
为定值(O为坐标原点)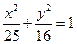 的右焦点,点A(4,1)是椭圆内的一点,点P(x,
的右焦点,点A(4,1)是椭圆内的一点,点P(x,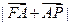 的最大值是
的最大值是  的离心率等于__________,与该椭圆有共
的离心率等于__________,与该椭圆有共
 的双曲线方程是
的双曲线方程是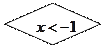
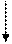

 ___________________.
___________________.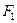 、
、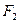 ,它们在第一象限
,它们在第一象限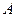 ,且
,且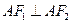 ,
,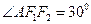 ,则椭圆与双曲
,则椭圆与双曲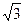

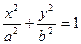 (a>b>0)的离心率
(a>b>0)的离心率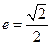 , 直线
, 直线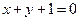 与椭圆交于P,Q两点, 且OP⊥OQ(如图) .
与椭圆交于P,Q两点, 且OP⊥OQ(如图) .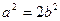 ;
;