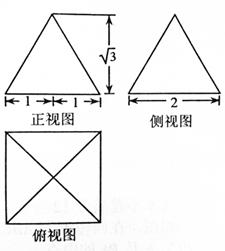
题目内容
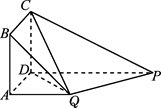
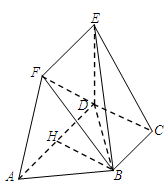
如图,在五面体 中,已知
中,已知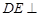 平面
平面 ,
,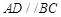 ,
,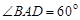 ,
,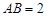 ,
,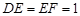 .
.
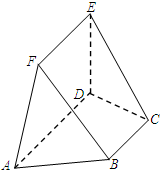
(1)求证: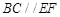 ;
;
(2)求三棱锥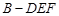 的体积.
的体积.
 中,已知
中,已知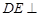 平面
平面 ,
,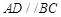 ,
,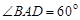 ,
,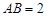 ,
,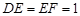 .
.
(1)求证:
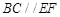 ;
;(2)求三棱锥
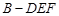 的体积.
的体积.(1)详见解析,(2)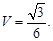
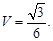
试题分析:(1)证明线线平行,一般思路为利用线面平行的性质定理与判定定理进行转化. 因为
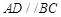 ,
, 平面
平面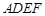 ,
, 平面
平面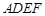 ,所以
,所以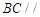 平面
平面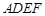 ,又
,又 平面
平面 ,平面
,平面 平面
平面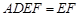 ,所以
,所以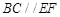 .(2)求三棱锥的体积,关键是找寻高.可由面面垂直性质定理探求,因为
.(2)求三棱锥的体积,关键是找寻高.可由面面垂直性质定理探求,因为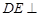 平面
平面 ,所以有面
,所以有面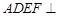 平面
平面 ,则作
,则作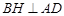 就可得
就可得 平面
平面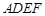 .证明
.证明 平面
平面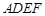 过程也可从线线垂直证线面垂直.确定
过程也可从线线垂直证线面垂直.确定 是三棱锥
是三棱锥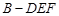 的高之后,可利用三棱锥
的高之后,可利用三棱锥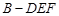 的体积公式
的体积公式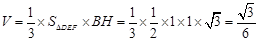 .
.试题解析:
(1)因为
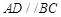 ,
, 平面
平面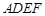 ,
, 平面
平面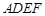 ,
,所以
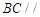 平面
平面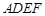 , 3分
, 3分又
 平面
平面 ,平面
,平面 平面
平面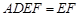 ,
,所以
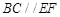 . 6分
. 6分(2)在平面
 内作
内作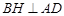 于点
于点 ,
,因为
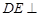 平面
平面 ,
,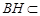 平面
平面 ,所以
,所以 ,
,又
 ,
, 平面
平面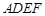 ,
,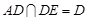 ,
,所以
 平面
平面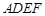 ,
,所以
 是三棱锥
是三棱锥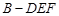 的高. 9分
的高. 9分在直角三角形
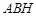 中,
中,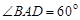 ,
,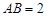 ,所以
,所以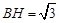 ,
,因为
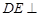 平面
平面 ,
, 平面
平面 ,所以
,所以 ,
,又由(1)知,
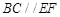 ,且
,且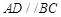 ,所以
,所以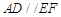 ,所以
,所以 , 12分
, 12分所以三棱锥
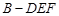 的体积
的体积 . 14分
. 14分
练习册系列答案
相关题目
 的棱长为2,E、F分别是
的棱长为2,E、F分别是 、
、 的中点,过
的中点,过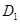 、E、F作平面
、E、F作平面 交
交 于G.
于G. ;
; 的余弦值;
的余弦值; 的体积.
的体积.
 的正三棱锥
的正三棱锥 中,
中, 长为
长为 ,
, 为棱
为棱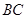 的中点,求
的中点,求
 与
与 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);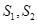 ,体积为
,体积为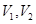 ,若它们的侧面积相等且
,若它们的侧面积相等且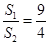 ,则
,则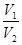 的值是 .
的值是 .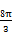
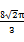
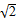 π
π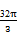
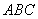 中,
中, 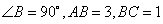 ,以边
,以边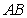 所在直线为旋转轴,其余各边旋转一周而形成的曲面所围成的几何体的体积为( )
所在直线为旋转轴,其余各边旋转一周而形成的曲面所围成的几何体的体积为( )