题目内容
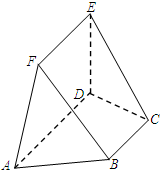
如图,在体积为 的正三棱锥
的正三棱锥 中,
中, 长为
长为 ,
, 为棱
为棱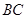 的中点,求
的中点,求

(1)异面直线 与
与 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
(2)正三棱锥 的表面积.
的表面积.
 的正三棱锥
的正三棱锥 中,
中, 长为
长为 ,
, 为棱
为棱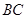 的中点,求
的中点,求
(1)异面直线
 与
与 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);(2)正三棱锥
 的表面积.
的表面积.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)本题求异面直线所成的角,根据定义要把这个角作出来,一般平移其中一条,到与另一条相交为此,题中由于有
 的中点
的中点 ,因此我们以
,因此我们以 中点
中点 ,就有
,就有 ,那么
,那么 就是所求的角(或其补角);(2)要求正三棱锥的表面积,必须求得斜高,由已知体积,可以先求得棱锥的高,取
就是所求的角(或其补角);(2)要求正三棱锥的表面积,必须求得斜高,由已知体积,可以先求得棱锥的高,取 的中心
的中心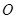 ,那么
,那么 就是棱锥的高,下面只要根据正棱锥的性质(正棱锥中的直角三角形)应该能求得侧棱长或斜高,有了斜高,就能求得棱锥的侧面积了,再加上底面积,就得到表面积了.
就是棱锥的高,下面只要根据正棱锥的性质(正棱锥中的直角三角形)应该能求得侧棱长或斜高,有了斜高,就能求得棱锥的侧面积了,再加上底面积,就得到表面积了.试题解析:(1)过点
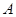 作
作 平面
平面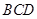 ,垂足为
,垂足为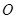 ,则
,则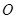 为
为 的中心,由
的中心,由 得
得 (理1分文2分)
(理1分文2分)又在正三角形
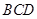 中得
中得 ,所以
,所以 (理2分文4分)
(理2分文4分)取
 中点
中点 ,连结
,连结 、
、 ,故
,故 ∥
∥ ,
,所以
 就是异面直线
就是异面直线 与
与 所成的角.(理4分文6分)
所成的角.(理4分文6分)在△
 中,
中, ,
, , (理5分文8分)
, (理5分文8分)所以
 . (理6分文10分)
. (理6分文10分)所以,异面直线
 与
与 所成的角的大小为
所成的角的大小为 . (理7分文12分)
. (理7分文12分)
(2)由
 可得正三棱锥
可得正三棱锥 的侧面积为
的侧面积为 (理10分)
(理10分)所以正三棱锥
 的表面积为
的表面积为 . (理12分)
. (理12分)
练习册系列答案
相关题目
 中,已知
中,已知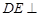 平面
平面 ,
,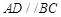 ,
,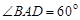 ,
,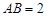 ,
,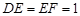 .
.
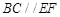 ;
;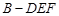 的体积.
的体积. 中,
中, 是等边三角形,
是等边三角形, .
.
 ;
; ;
; ,且平面
,且平面 平面
平面 ,求三棱锥
,求三棱锥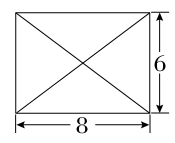
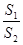 =________.
=________. 中,
中, 则四面体外接球的表面积为( )
则四面体外接球的表面积为( )
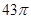





 的五个顶点都在一个球面上,且底面ABCD是边长为1的正方形,
的五个顶点都在一个球面上,且底面ABCD是边长为1的正方形, ,
,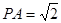 ,则该球的体积为 _
,则该球的体积为 _