题目内容

6．已知等差数列{an}的前n项和为Sn，若m＞1，且am-1+am+1-am-1=0，S2m-1=39．则m等于（　　）
A．19B．39C．10D．20

分析 由等差数列的性质和已知可得am=1，再由求和公式和性质可得S2m-1=$\frac{（2m-1）（{a}_{1}+{a}_{2m-1}）}{2}$=（2m-1）am=39，代值解关于m的方程可得．

解答 解：∵am-1+am+1-am-1=0，
∴由等差数列的性质可得am-1+am+1=2am，
代入上式可得2am-am-1=0，解得am=1，
∴S2m-1=$\frac{（2m-1）（{a}_{1}+{a}_{2m-1}）}{2}$=39，
∴$\frac{（2m-1）×2{a}_{m}}{2}$=（2m-1）am=39，
∴2m-1=39，解得m=20
故选：D

点评 本题考查等差数列的求和公式和性质，属基础题．

练习册系列答案
相关题目
4．已知等差数列{an}通项公式an=4n-3．
（1）求{an}的前四项，
（2）求公差d；
（3）求前六项和S6．
17．已知P是抛物线C：y=x2上一点，则点P到直线y=x-3的最短距离为$\frac{11\sqrt{2}}{8}$．
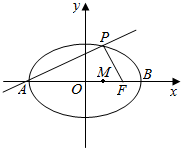14．如图所示，点A，B分别是椭圆$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{20}$=1长轴的左、右端点，点F是椭圆的右焦点，点P在椭圆上，且位于x轴上方，PA⊥PF，设M是椭圆长轴AB上的一点，M到直线AP的距离等于|MB|．
（1）求点P的坐标；
（2）求点M的坐标；
（3）求椭圆上的点到点M的距离d的最小值．
1．在△ABC中，角A，B，C所对的边分别为a，b，c，且8sin2（$\frac{A+B}{2}$）+3cos2C=3．
（1）求cosC；
（2）若B=$\frac{π}{2}$，2$\overrightarrow{AM}$=$\overrightarrow{MC}$，求tan∠ABM．
11．已知数列{an}的前n项和Sn=$\frac{1}{2}$n2+$\frac{1}{2}$n，
（1）求数列{an}的通项公式；
（2）令bn=$\frac{1}{{a}_{n}{a}_{n+1}}$，求数列{bn}的前2015项和T2015．
18．一个蜂巢里有1只蜜蜂，第1天，它飞出去找回了3个伙伴；第2天，4只蜜蜂飞出去，各自找回了3个伙伴如果这个找伙伴的过程继续下去，第6天所有的蜜蜂都归巢后，蜂巢中蜜蜂的总只数为（　　）
A．243B．729C．1024D．4096
15．在等差数列{an}中，$\frac{{a}_{9}}{{a}_{8}}$＜-1，若它的前n项和Sn有最大值，则使Sn＞0成立的最大自然数n的值为（　　）
A．15B．16C．17D．18
16．n=${∫}_{0}^{2}$（3x2-1）dx，则二项式（x-$\frac{1}{{x}^{2}}$）n展开式中的常数项为（　　）
A．15B．20C．25D．70

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网