题目内容

15．在等差数列{an}中，$\frac{{a}_{9}}{{a}_{8}}$＜-1，若它的前n项和Sn有最大值，则使Sn＞0成立的最大自然数n的值为（　　）
A．15B．16C．17D．18

分析 由题意可得a8＞0，a9＜0，且a8+a9＜0，由等差数列的性质和求和公式可得结论．

解答 解：∵前n项和Sn有最大值，∴公差d＜0，
又$\frac{{a}_{9}}{{a}_{8}}$＜-1，∴a8＞0，a9＜0，
∴由不等式的性质可得a8+a9＜0，
∴S15=$\frac{15（{a}_{1}+{a}_{15}）}{2}$=$\frac{15•2{a}_{8}}{2}$=15a8＞0，
S16=$\frac{16（{a}_{1}+{a}_{16}）}{2}$=8（a8+a9）＜0，
∴使Sn＞0成立的最大自然数n的值为：15．
故选：A．

点评 本题考查等差数列的性质，涉及等差数列的求和公式，属中档题．

练习册系列答案
相关题目
5．椭圆$\frac{x^2}{9}+{y^2}=1$的离心率e=$\frac{2\sqrt{2}}{3}$．
6．已知等差数列{an}的前n项和为Sn，若m＞1，且am-1+am+1-am-1=0，S2m-1=39．则m等于（　　）
A．19B．39C．10D．20
3．在△ABC中，a=3，A=30°，B=60°，则△ABC的面积S=$\frac{9\sqrt{3}}{2}$．
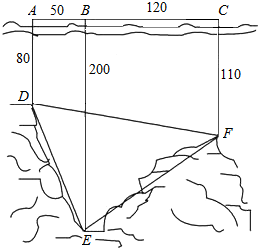10．马航MH370牵动全球人的心，世界各国积极投身到马航的搜救工作中，了解海底构造是救援工作要做的第一件事．某搜救队在某海域的海平面上的同一条直线上的A，B，C三点进行测量，得AB=50，BC=120，于A，B，C三处测得水深分别为AD=80，BE=200，CF=110，如图所示，试利用你所学知识求∠DEF的余弦值．
20．给出下列四个命题：
①椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，则b=c
②双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的焦点到渐近线的距离是b；
③已知抛物线y2=2px上两点A（x1，y1），B（x2，y2），且$\overrightarrow{OA}•\overrightarrow{OB}$=0（O为原点），则y1y2=-p2；
④动点M到两定点A、B的距离之比为常数λ（λ＞0且≠1），则动点M的轨迹是圆．
其中的真命题是①②④．（把你认为是真命题的序号都填上）
7．设随机变量ξ服从正态分布N（4，5），若P（ξ＜2a-3）=P（ξ＞a+2），则实数a等于（　　）
A．$\frac{7}{3}$B．$\frac{5}{3}$C．5D．3
4．复数i（1+i）等于（　　）
A．1+iB．1-iC．-1+iD．-1-i
5．“x＞1”是“$\frac{1}{x}＜1$”的（　　）
A．充要条件B．充分非必要条件
C．必要非充分条件D．既非充分又非必要条件

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网