题目内容
17.已知P是抛物线C:y=x2上一点,则点P到直线y=x-3的最短距离为$\frac{11\sqrt{2}}{8}$.分析 设P(m,m2),由点到直线的距离公式,可求P到直线x-y-3=0的距离,由二次函数的性质可求P到直线x-y-3=0的最小距离.
解答 解:设P(m,m2)
P到直线x-y-3=0的距离d=$\frac{|m-{m}^{2}-3|}{\sqrt{2}}$=$\frac{|(m-\frac{1}{2})^{2}+\frac{11}{4}|}{\sqrt{2}}$,
由二次函数的性质可知,当m=$\frac{1}{2}$时,最小距离d=$\frac{11\sqrt{2}}{8}$.
故答案为:$\frac{11\sqrt{2}}{8}$.
点评 本题考查直线与抛物线的位置关系的应用,解题时要注意公式的灵活运用,抛物线的基本性质和点到线的距离公式的应用,考查综合运用能力.

练习册系列答案
相关题目
12.已知定义在R上的函数f(x)满足f(x+1.5)=-f(x),当x∈[0,3)时,f(x)=|(x-1)2-0.5|,记集合A={n|n是函数y=f(x)(-3≤x≤5.5)的图象与直线y=m(m∈R)的交点个数},则集合A的子集个数为( )
| A. | 8 | B. | 16 | C. | 32 | D. | 64 |
2.命题“?x∈R,ex>x2”的否定是( )
| A. | 不存在x∈R,使ex>x2 | B. | ?x0∈R,使ex0<x02 | ||
| C. | ?x0∈R,使ex0≤x02 | D. | ?x∈R,使ex≤x2 |
6.已知等差数列{an}的前n项和为Sn,若m>1,且am-1+am+1-am-1=0,S2m-1=39.则m等于( )
| A. | 19 | B. | 39 | C. | 10 | D. | 20 |
7.设随机变量ξ服从正态分布N(4,5),若P(ξ<2a-3)=P(ξ>a+2),则实数a等于( )
| A. | $\frac{7}{3}$ | B. | $\frac{5}{3}$ | C. | 5 | D. | 3 |
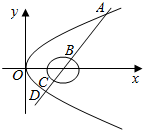 如图,直线y=x-2与圆x2+y2-4x+3=0及抛物线y2=8x依次交于A、B、C、D四点,则|AB|+|CD|=14.
如图,直线y=x-2与圆x2+y2-4x+3=0及抛物线y2=8x依次交于A、B、C、D四点,则|AB|+|CD|=14.