题目内容
1.已知函数$f(x)=a(x-\frac{1}{x})-2lnx(a∈R)$,g(x)=-$\frac{a}{x}$,若至少存在一个x0∈[1,e],使f(x0)>g(x0)成立,则实数a的范围为( )| A. | [$\frac{2}{e}$,+∞) | B. | (0,+∞) | C. | [0,+∞) | D. | ($\frac{2}{e}$,+∞) |
分析 由题意得:f(x)-g(x)>0在[1,e]上有解,分离参数,求最值,即可求出实数a的范围.
解答 解:由题意得:f(x)-g(x)>0在[1,e]上有解,
即$ax-2lnx>0,a>{(\frac{2lnx}{x})_{min}}$,
设$y=\frac{2lnx}{x}$,则$y'=\frac{2(1-lnx)}{x^2}≥0$,
因此当x=1时,${(\frac{2lnx}{x})_{min}}=0,a>0$,
故选:B.
点评 本题考查导数知识的综合运用,考查学生等价转化问题的能力,转化为f(x)-g(x)>0在[1,e]上有解,分离参数,求最值是关键.

练习册系列答案
相关题目
11.方程$\frac{x^2}{k-4}+\frac{y^2}{10-k}$=1表示焦点在x轴上的椭圆,则实数k的取值范围是( )
| A. | (4,+∞) | B. | (4,7) | C. | (7,10) | D. | (4,10) |
13.如图,若执行该程序,输出结果为48,则输入k值为( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
10.已知点P是边长为4的正方形内任一点,则点P到四个顶点的距离均大于2的概率是( )
| A. | $\frac{π}{4}$ | B. | 1-$\frac{π}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{π}{3}$ |
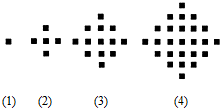 某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.