题目内容
11.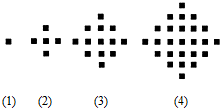 某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.(1)求出f(2),f(3)f(4)f(5)并猜测f(n)的表达式;
(2)求证:$\frac{1}{f(1)}$+$\frac{1}{f(2)-1}$+$\frac{1}{f(3)-1}$+…+$\frac{1}{f(n)-1}$$<\frac{3}{2}$.
分析 (1)先分别观察给出正方体的个数为:1,1+4,1+4+8,…,即可求出f(2),f(3),f(4),f(5);总结一般性的规律,可知f(n+1)-f(n)=4n,利用叠加法,可求f(n)的表达式;
(2)根据通项特点,利用裂项法求和,结合数列的单调性即可得证.
解答 解:(1)∵f(1)=1,
f(2)=5,
f(3)=13,
f(4)=25,
∴f(5)=25+4×4=41.
∵f(2)-f(1)=4=4×1,
f(3)-f(2)=8=4×2,
f(4)-f(3)=12=4×3,
f(5)-f(4)=16=4×4,
由上式规律得出f(n+1)-f(n)=4n.
∴f(n)-f(n-1)=4(n-1),
f(n-1)-f(n-2)=4•(n-2),
f(n-2)-f(n-3)=4•(n-3),
…
f(2)-f(1)=4×1,
∴f(n)-f(1)=4[(n-1)+(n-2)+…+2+1]=2(n-1)•n,
∴f(n)=2n2-2n+1(n≥2),
又n=1时,f(1)也适合f(n).
∴f(n)=2n2-2n+1.--------(6分)
证明:(2)当n≥2时,$\frac{1}{f(n)-1}$=$\frac{1}{2{n}^{2}-2n+1-1}$=$\frac{1}{2}$($\frac{1}{n-1}-\frac{1}{n}$),
∴$\frac{1}{f(1)}$+$\frac{1}{f(2)-1}$+$\frac{1}{f(3)-1}$+…+$\frac{1}{f(n)-1}$=1+$\frac{1}{2}$(1-$\frac{1}{2}+\frac{1}{2}-\frac{1}{3}$+…+$\frac{1}{n-1}-\frac{1}{n}$)=1+$\frac{1}{2}$(1-$\frac{1}{n}$)=$\frac{3}{2}$-$\frac{1}{2n}$<$\frac{3}{2}$
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案| A. | [$\frac{2}{e}$,+∞) | B. | (0,+∞) | C. | [0,+∞) | D. | ($\frac{2}{e}$,+∞) |
| A. | $\frac{4}{5}$ | B. | $\frac{5}{4}$ | C. | -$\frac{4}{5}$ | D. | -$\frac{5}{4}$ |
| 分组 | 频数累计 | 频数 | 频率 |
| [10.75,10.85) | 6 | 6 | 0.06 |
| [10.85,10.95) | 15 | 9 | 0.09 |
| [10.95,11.05) | 30 | 15 | 0.15 |
| [11.05,11.15) | 48 | 18 | 0.18 |
| [11.15,11.25) | |||
| [11.25,11.35) | 84 | 12 | 0.12 |
| [11.35,11.45) | 92 | 8 | 0.08 |
| [11.45,11.55) | 98 | 6 | 0.06 |
| [11.55,11.65) | 100 | 2 | 0.02 |
(Ⅱ)画出频率分布直方图;
(Ⅲ)据上述图表,估计产品直径落在[10.95,11.35)范围内的可能性是百分之几?
(Ⅳ)从[11.35,11.45)∪[11.55,11.65)中抽取两个产品,直径分别记作为x,y,求|x-y|<0.1的概率

| A. | 增函数 | B. | 减函数 | C. | 奇函数 | D. | 偶函数 |
| A. | $\frac{{x}^{2}}{10}$+$\frac{{y}^{2}}{15}$=1 | B. | $\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{10}$=1 | C. | $\frac{{x}^{2}}{15}$+$\frac{{y}^{2}}{10}$=1 | D. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{10}$=1 |
| A. | $\frac{π}{2}$ | B. | π | ||
| C. | 2π | D. | 与a的值的大小有关 |