题目内容
【题目】已知曲线C的参数方程是 ![]() (θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,A、B的极坐标分别为A﹣(2,0)、B(﹣1,
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,A、B的极坐标分别为A﹣(2,0)、B(﹣1, ![]() )
)
(1)求直线AB的直角坐标方程;
(2)在曲线C上求一点M,使点M到AB的距离最大,并求出些最大值.
【答案】
(1)解:由题意A(﹣2,0),B(﹣1,﹣ ![]() ),∴kAB=﹣
),∴kAB=﹣ ![]() ,
,
∴直线AB的方程为y﹣0=﹣ ![]() (x+2),即
(x+2),即 ![]() x+y+2
x+y+2 ![]() =0
=0
(2)解:设M(2cosθ,2sinθ)(θ∈(0,2π],M到直线AB的距离d= ![]() =
= ![]() ,
,
∴sin(θ+ ![]() )=1,即
)=1,即 ![]() ,dmax=2+
,dmax=2+ ![]() ,此时M(
,此时M( ![]() ,1)
,1)
【解析】(1)求出直线的斜率,即可求直线AB的直角坐标方程;(2)设M(2cosθ,2sinθ)(θ∈(0,2π],M到直线AB的距离d= ![]() =
= ![]() ,即可得出结论.
,即可得出结论.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】下表是最近十届奥运会的年份、届别、主办国,以及主办国在上届获得的金牌数、当届
获得的金牌数的统计数据:
年份 | 1972 | 1976 | 1980 | 1984 | 1988 | 1992 | 1996 | 2000 | 2004 | 2008 |
届别 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
主办国家 | 联邦 德国 | 加拿大 | 苏联 | 美国 | 韩国 | 西班牙 | 美国 | 澳大 利亚 | 希腊 | 中国 |
上届金牌数 | 5 | 0 | 49 | 未参加 | 6 | 1 | 37 | 9 | 4 | 32 |
当界金牌数 | 13 | 0 | 80 | 83 | 12 | 13 | 44 | 16 | 6 | 51 |
某体育爱好组织,利用上表研究所获金牌数与主办奥运会之间的关系,
(1)求出主办国在上届所获金牌数(设为![]() )与在当届所获金牌数(设为
)与在当届所获金牌数(设为![]() )之间的线性回归方程
)之间的线性回归方程
![]() 其中
其中![]()
(2)在2008年第29届北京奥运会上日本获得9块金牌,则据此线性回归方程估计在2020 年第 32 届东
京奥运会上日本将获得的金牌数为(所有金牌数精确到整数)
【题目】某校某次N名学生的学科能力测评成绩(满分120分)的频率分布直方图如下,已知分数在100﹣110的学生数有21人
(1)求总人数N和分数在110﹣115分的人数n.;
(2)现准备从分数在110﹣115的n名学生(女生占 ![]() )中选3位分配给A老师进行指导,设随机变量ξ表示选出的3位学生中女生的人数,求ξ的分布列与数学期望Eξ;
)中选3位分配给A老师进行指导,设随机变量ξ表示选出的3位学生中女生的人数,求ξ的分布列与数学期望Eξ;
(3)为了分析某个学生的学习状态,对其下一阶段的学习提供指导建议,对他前7次考试的数学成绩x、物理成绩y进行分析,该生7次考试成绩如表
数学(x) | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理(y) | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
已知该生的物理成绩y与数学成绩x是线性相关的,求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() .若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少?
.若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少?
附:对于一组数据(x1 , y1),(x2 , y2),…,(xn , yn),其回归方程 ![]() =
= ![]() x+
x+ ![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ![]() =
= 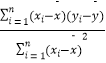 ,
, ![]() .
.