题目内容
【题目】某校某次N名学生的学科能力测评成绩(满分120分)的频率分布直方图如下,已知分数在100﹣110的学生数有21人
(1)求总人数N和分数在110﹣115分的人数n.;
(2)现准备从分数在110﹣115的n名学生(女生占 ![]() )中选3位分配给A老师进行指导,设随机变量ξ表示选出的3位学生中女生的人数,求ξ的分布列与数学期望Eξ;
)中选3位分配给A老师进行指导,设随机变量ξ表示选出的3位学生中女生的人数,求ξ的分布列与数学期望Eξ;
(3)为了分析某个学生的学习状态,对其下一阶段的学习提供指导建议,对他前7次考试的数学成绩x、物理成绩y进行分析,该生7次考试成绩如表
数学(x) | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理(y) | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
已知该生的物理成绩y与数学成绩x是线性相关的,求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() .若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少?
.若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少?
附:对于一组数据(x1 , y1),(x2 , y2),…,(xn , yn),其回归方程 ![]() =
= ![]() x+
x+ ![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ![]() =
= 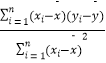 ,
, ![]() .
.
【答案】
(1)解:分数在100﹣110内的学生的频率为P1=(0.04+0.03)×5=0.35,
所以该班总人数为N= ![]() =60,
=60,
分数在110﹣115内的学生的频率为
P2=1﹣(0.01+0.04+0.05+0.04+0.03+0.01)×5=0.1,
分数在110﹣115内的人数为n=60×0.1=6
(2)解:由题意分数在110﹣115内有6名学生,其中女生有2名,
从6名学生中选出3人,女生人数ξ的可能取值为0,1,2;
则P(ξ=0)= ![]() =
= ![]() ,P(ξ=1)=
,P(ξ=1)= ![]() =
= ![]() ,P(ξ=2)=
,P(ξ=2)= ![]() =
= ![]() ;
;
所以ξ的分布列为:
ξ | 0 | 1 | 2 |
P |
|
|
|
ξ的数学期望为Eξ=0× ![]() +1×
+1× ![]() +2×
+2× ![]() =1
=1
(3)解:计算 ![]() =
= ![]() ×(88+83+117+92+108+100+112)=100,
×(88+83+117+92+108+100+112)=100,
![]() =
= ![]() ×(94+91+108+96+104+101+106)=100;
×(94+91+108+96+104+101+106)=100;
由于x与y之间具有线性相关关系,
根据回归系数公式得到 ![]() =
= 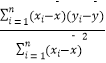 =
= ![]() =0.5,
=0.5,
![]() =100﹣0.5×100=50,
=100﹣0.5×100=50,
∴线性回归方程为 ![]() =0.5x+50,
=0.5x+50,
∴当x=130时, ![]() =0.5×130+50=115
=0.5×130+50=115
【解析】(1)根据题意,计算分数在100﹣110内的频率,求出该班总人数,再计算分数在110﹣115内的频率,计算对应的人数;(2)求出分数6名学生中女生有2名,得出6名学生中选出3人,女生人数ξ的可能取值,再计算对应的概率值,写出ξ的分布列,计算数学期望值;(3)计算 ![]() 、
、 ![]() ,求出回归系数
,求出回归系数 ![]() 、写出对应线性回归方程,根据方程计算x=130时
、写出对应线性回归方程,根据方程计算x=130时 ![]() 的值即可.
的值即可.

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案【题目】对一个样本容量为100的数据分组,各组的频数如表:
区间 | [17,19) | [19,21) | [21,23) | [23,25) | [25,27) | [27,29) | [29,31) | [31,33] |
频数 | 1 | 1 | 3 | 3 | 18 | 16 | 28 | 30 |
估计小于29的数据大约占总体的( )
A. 16% B. 40% C. 42% D. 58%
【题目】某校为了分析本校高中生的性别与是否喜欢数学之间的关系,在高中生中随机地抽取了90名学生调查,得到了如下列联表:
喜欢数学 | 不喜欢数学 | 总计 | |
男 | 30 | ① | 45 |
女 | ② | 25 | 45 |
总计 | ③ | ④ | 90 |
(1)求①②③④处分别对应的值;
(2)能有多大把握认为“高中生的性别与喜欢数学”有关?
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() .
.