题目内容
10．已知a，b∈R，则“$\sqrt{a-1}$＞$\sqrt{b-1}$”是“log2a＞log2b”的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
分析 分别解出关于$\sqrt{a-1}$＞$\sqrt{b-1}$以及log2a＞log2b”的a，b的范围，从而得到答案．
解答 解：由$\sqrt{a-1}$＞$\sqrt{b-1}$，解得：a＞b≥1，
由log2a＞log2b解得：a＞b＞0，
故“$\sqrt{a-1}$＞$\sqrt{b-1}$”是“log2a＞log2b”的充分不必要条件，
故选：A．
点评 本题考察了充分必要条件，考察二次函数以及对数函数的性质，是一道基础题．
练习册系列答案
出彩同步大试卷系列答案
相关题目
20．椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$和椭圆$\frac{x^2}{25-m}+\frac{y^2}{9-m}=1$具有（ ）
| A． | 相同的离心率 | B． | 相同的焦点 | C． | 相同的顶点 | D． | 相同的长、短轴 |
1．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）过点P（3，1），其左、右焦点分别为F1、F2，且$\overrightarrow{{F}_{1}P}$•$\overrightarrow{{F}_{2}P}$=-6，则椭圆E的离心率是（ ）
| A． | $\frac{\sqrt{2}}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{2\sqrt{2}}{3}$ |
2．
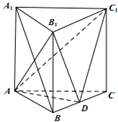如图，三棱柱ABC-A1B1C1的侧棱垂直于底面，底面边长和侧棱长均为2，D是BC的中点．
（Ⅰ）求证：AD⊥平面B1BCC1；
（Ⅱ）求证：A1B∥平面ADC1；
（Ⅲ）求三棱锥C1-ADB1的体积．
如图，三棱柱ABC-A1B1C1的侧棱垂直于底面，底面边长和侧棱长均为2，D是BC的中点．（Ⅰ）求证：AD⊥平面B1BCC1；
（Ⅱ）求证：A1B∥平面ADC1；
（Ⅲ）求三棱锥C1-ADB1的体积．
19．等比数列{an}中，任意的n∈N*，an+1+an=3n+1，则公比q等于（ ）
| A． | 2 | B． | 3 | C． | $\sqrt{3}$ | D． | -$\sqrt{3}$ |