题目内容
18.对于函数f(x),若存在区间A=[m,n],使得{y|y=f(x),x∈A}=A,则称函数f(x)为“可等域函数”,区间A为函数f(x)的一个“可等域区间”,给出下列四个函数:①f(x)=sin$\frac{π}{2}$x;②f(x)=2x2-1;③f(x)=|1-2x|;④f(x)=lnx+1.
其中存在“可等域区间”的“可等域函数”为①②③.
分析 结合题意,分别写出①f(x)=sin$\frac{π}{2}$x;②f(x)=2x2-1;③f(x)=|1-2x|的可等域区间,④判断f(x)=lnx+1没有可等域区间.
解答 解:①f(x)=sin$\frac{π}{2}$x的可等域区间有[0,1];
②f(x)=2x2-1的可等域区间有[-1,1];
③f(x)=|1-2x|的可等域区间有[0,1];
④f(x)=lnx+1是增函数,
故令lnx+1=x,
解得,x=1;
故f(x)=lnx+1没有可等域区间.
故答案为:①②③.
点评 本题考查了函数的性质的判断与应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.已知函数f(x)=sin(2x+φ)(|φ|<$\frac{π}{2}$),且f($\frac{π}{12}$)=1,为了得到g(x)=sin2x的图象,则只要将f(x)的图象( )
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
10.已知a,b∈R,则“$\sqrt{a-1}$>$\sqrt{b-1}$”是“log2a>log2b”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
7.已知向量$\overrightarrow{OA}$=(k,12),$\overrightarrow{OB}$=(4,5),$\overrightarrow{OC}$=(-k,10),且A、B、C三点共线,则k=( )
| A. | -$\frac{4}{3}$ | B. | $\frac{4}{3}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
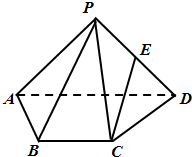 如图,四棱锥P-ABCD中,PA⊥PD,AD⊥CD,PA=PD,AD∥BC,AB=AD=2BC=2,E是棱PD的中点,设二面角P-AD-B的值为θ.
如图,四棱锥P-ABCD中,PA⊥PD,AD⊥CD,PA=PD,AD∥BC,AB=AD=2BC=2,E是棱PD的中点,设二面角P-AD-B的值为θ.