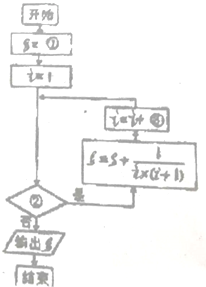
题目内容

20．设函数f（x）=（x+sinx）（ex+ae-x）（x∈R）是偶函数，则实数a=-1．

分析 由题意得（x+sinx）（ex+ae-x）=（-x+sin（-x））（e-x+aex），从而化简求得．

解答 解：∵函数f（x）=（x+sinx）（ex+ae-x）（x∈R）是偶函数，
∴（x+sinx）（ex+ae-x）=（-x+sin（-x））（e-x+aex），
∴ex+ae-x=-（e-x+aex）；
a（e-x+ex）=-（e-x+ex）；
故a=-1；
故答案为：-1．

点评 本题考查了函数的奇偶性的判断与应用，属于基础题．

练习册系列答案
相关题目
10．已知a，b∈R，则“$\sqrt{a-1}$＞$\sqrt{b-1}$”是“log2a＞log2b”的（　　）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件
11．设某高校高三女生体重y（单位：kg）与身高x（单位：cm）具有线性关系，根据一组样本数据（xi，yi）（i=1，2，…n），用最小二乘法求得的回归直线方程为$\widehat{y}$=0.85x-85.71，若该校高三某女生身高增加1cm，则其体重约增加0.85kg．
8．已知：命题p：椭圆$\frac{{x}^{2}}{m+1}$+$\frac{{y}^{2}}{2-m}$=1的焦点在x轴上，命题q：不等式x2+2xy≤m（2x2+y2）对于一切整数x，y恒成立．
（1）若p为假命题，求实数m的取值范围；
（2）若p∧q是假命题，p∨q是真命题，求实数m的取值范围．
15．设α、β是两个不同的平面，l、m为两条不同的直线，命题p：若α∥β，l?α，m?β，则l∥m，命题q：l∥α，m⊥l，m?β，则α⊥β则下列命题为真命题的是（　　）
A．p∨qB．p∧qC．（￢p）∨qD．p∧（￢q）
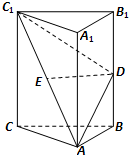5．如图，在直三棱柱ABC-A1B1C1中，AB=BC，D，E分别为BB1，AC1的中点．
（1）证明：DE⊥平面ACC1A1；
（2）设AA1=AC=$\sqrt{2}$AB，求二面角A1-AD-C1的大小．
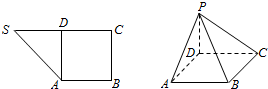12．如图1，在直角梯形SABC中，∠B=∠C=$\frac{π}{2}$，D为边SC上的点，且AD⊥SC，现将△SAD沿AD折起到达PAD的位置（折起后点S记为P），并使得PA⊥AB．
（1）求证：PD⊥平面ABCD；
（2）已知PD=AD，PD+AD+DC=6，当线段PB取得最小值时，请解答以下问题：
①设点E满足$\overrightarrow{BE}$=λ$\overrightarrow{BP}$（0≤λ≤1），则是否存在λ，使得平面EAC与平面PDC所成的锐角是$\frac{π}{3}$？若存在，求出λ；若不存在，请说明理由；
②设G是AD的中点，则在平面PBC上是否存在点F，使得FG⊥平面PBC？若存在，确定点F的位置，若不存在，请说明理由．
9．${（1-\sqrt{x}）^5}$的展开式中x2的系数是（　　）
A．-5B．5C．-10D．10
10．如图是求$\frac{1}{1×2}$+$\frac{1}{3×4}$+$\frac{1}{5×6}$+…+$\frac{1}{101×102}$值的程序框图，回答下列问题．

（1）该算法使用的是什么循环结构？
（2）分别在①、②、③处填上合适的语句，使之能完成该题的算法功能．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网