题目内容
20.椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$和椭圆$\frac{x^2}{25-m}+\frac{y^2}{9-m}=1$具有( )| A. | 相同的离心率 | B. | 相同的焦点 | C. | 相同的顶点 | D. | 相同的长、短轴 |
分析 分别计算出各自的焦距,结合焦点均在x轴上,即得结论.
解答 解:∵椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$的焦距为:2$\sqrt{25-9}$=8,
圆$\frac{x^2}{25-m}+\frac{y^2}{9-m}=1$的焦距为:2$\sqrt{(25-m)-(9-m)}$=8,
椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$和椭圆$\frac{x^2}{25-m}+\frac{y^2}{9-m}=1$的焦点均在x轴上,
∴两椭圆有相同的焦点,
故选:B.
点评 本题考查椭圆的简单性质,注意解题方法的积累,属于基础题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
5.设椭圆C1的离心率为$\frac{5}{13}$,焦点在x轴上,且长轴长为26,若曲线C2上的点到椭圆C1的两个焦点的距离的差的绝对值等于8,则曲线C2的标准方程为( )
| A. | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | B. | $\frac{x^2}{169}-\frac{y^2}{144}=1$ | C. | $\frac{x^2}{16}+\frac{y^2}{9}=1$ | D. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ |
10.已知a,b∈R,则“$\sqrt{a-1}$>$\sqrt{b-1}$”是“log2a>log2b”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
 椭圆E:$\frac{{x}^{2}}{4}$+y2=1的左、右焦点分别为F1,F2,左、右顶点分别为A,B.
椭圆E:$\frac{{x}^{2}}{4}$+y2=1的左、右焦点分别为F1,F2,左、右顶点分别为A,B.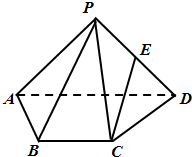 如图,四棱锥P-ABCD中,PA⊥PD,AD⊥CD,PA=PD,AD∥BC,AB=AD=2BC=2,E是棱PD的中点,设二面角P-AD-B的值为θ.
如图,四棱锥P-ABCD中,PA⊥PD,AD⊥CD,PA=PD,AD∥BC,AB=AD=2BC=2,E是棱PD的中点,设二面角P-AD-B的值为θ.