题目内容
19.等比数列{an}中,任意的n∈N*,an+1+an=3n+1,则公比q等于( )| A. | 2 | B. | 3 | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
分析 把n=1、2分别代入已知的式子,并利用等比数列的通项公式化简求出公比q的值.
解答 解:∵等比数列{an}中,任意的n∈N*,an+1+an=3n+1,
∴a2+a1=32,a3+a2=qa2+qa1=33,
两个式子相除可得,公比q=3,
故选:B.
点评 本题考查了等比数列的通项公式,以及递推公式的化简,属于基础题.

练习册系列答案
相关题目
10.已知a,b∈R,则“$\sqrt{a-1}$>$\sqrt{b-1}$”是“log2a>log2b”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
7.已知向量$\overrightarrow{OA}$=(k,12),$\overrightarrow{OB}$=(4,5),$\overrightarrow{OC}$=(-k,10),且A、B、C三点共线,则k=( )
| A. | -$\frac{4}{3}$ | B. | $\frac{4}{3}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
9.${(1-\sqrt{x})^5}$的展开式中x2的系数是( )
| A. | -5 | B. | 5 | C. | -10 | D. | 10 |
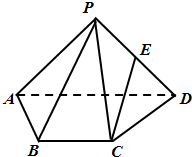 如图,四棱锥P-ABCD中,PA⊥PD,AD⊥CD,PA=PD,AD∥BC,AB=AD=2BC=2,E是棱PD的中点,设二面角P-AD-B的值为θ.
如图,四棱锥P-ABCD中,PA⊥PD,AD⊥CD,PA=PD,AD∥BC,AB=AD=2BC=2,E是棱PD的中点,设二面角P-AD-B的值为θ.