题目内容
2．
如图，三棱柱ABC-A1B1C1的侧棱垂直于底面，底面边长和侧棱长均为2，D是BC的中点．（Ⅰ）求证：AD⊥平面B1BCC1；
（Ⅱ）求证：A1B∥平面ADC1；
（Ⅲ）求三棱锥C1-ADB1的体积．
分析 （Ⅰ）证明AD⊥平面B1BCC1，利用线面垂直的判定，证明CC1⊥AD，BC⊥AD，即可‘
（Ⅱ）连接A1C，交AC1于点O，连接OD，利用OD为△A1BC中位线，可得A1B∥OD，利用线面平行的判定，可证A1B∥平面ADC1；
（Ⅲ）转换底面，利用棱锥的体积公式，即可求三棱锥C1-ADB1的体积．
解答 （Ⅰ）证明：因为ABC-A1B1C1是正三棱柱，所以CC1⊥平面ABC
因为AD?平面ABC，所以CC1⊥AD
因为△ABC是正三角形，D为BC中点，所以BC⊥AD，
因为CC1∩BC=C，所以AD⊥平面B1BCC1．
（Ⅱ）证明：连接A1C，交AC1于点O，连接OD．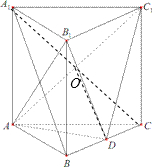
由 ABC-A1B1C1是正三棱柱，得四边形ACC1A1为矩形，O为A1C的中点．
又D为BC中点，所以OD为△A1BC中位线，
所以A1B∥OD，
因为A1B?平面ADC1，OD?平面ADC1，
所以A1B∥平面ADC1；
（Ⅲ）解：三棱锥C1-ADB1的体积=${V}_{A-{C}_{1}D{B}_{1}}$=$\frac{1}{3}{S}_{△{B}_{1}D{C}_{1}}•AD$=$\frac{2\sqrt{3}}{3}$．
点评 本题考查线面垂直，考查线面平行，考查三棱锥体积的计算，掌握线面垂直、线面平行的判定是关键．
练习册系列答案
相关题目
椭圆E：$\frac{{x}^{2}}{4}$+y2=1的左、右焦点分别为F1，F2，左、右顶点分别为A，B．
13．已知函数f（x）=sin（2x+φ）（|φ|＜$\frac{π}{2}$），且f（$\frac{π}{12}$）=1，为了得到g（x）=sin2x的图象，则只要将f（x）的图象（ ）
| A． | 向左平移$\frac{π}{3}$个单位 | B． | 向右平移$\frac{π}{3}$个单位 | ||
| C． | 向左平移$\frac{π}{6}$个单位 | D． | 向右平移$\frac{π}{6}$个单位 |
10．已知a，b∈R，则“$\sqrt{a-1}$＞$\sqrt{b-1}$”是“log2a＞log2b”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
17．若直线ax-y+1=0与直线2x+y+2=0平行，则a的值为（ ）
| A． | -2 | B． | -1 | C． | $\frac{1}{2}$ | D． | 1 |
7．已知向量$\overrightarrow{OA}$=（k，12），$\overrightarrow{OB}$=（4，5），$\overrightarrow{OC}$=（-k，10），且A、B、C三点共线，则k=（ ）
| A． | -$\frac{4}{3}$ | B． | $\frac{4}{3}$ | C． | -$\frac{2}{3}$ | D． | $\frac{2}{3}$ |
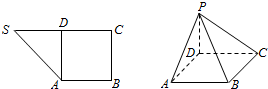如图1，在直角梯形SABC中，∠B=∠C=$\frac{π}{2}$，D为边SC上的点，且AD⊥SC，现将△SAD沿AD折起到达PAD的位置（折起后点S记为P），并使得PA⊥AB．