题目内容
15.已知圆:x2+y2=64,圆C与圆O相交,圆心为C(9,0),且圆C上的点与圆O上的点之间的最大距离为21.(Ⅰ)求圆C的标准方程;
(Ⅱ)在x轴上是否存在定点P,使得过点P的直线l被圆O与圆C截得的弦长d1、d2的比值总等于同一常数λ?若存在,求点P的坐标及λ的值,若不存在,说明理由.
分析 (1)圆O1的半径为4,圆心为O1(9,0),从而可得圆O1的标准方程;
(2)当直线l的斜率存在时,设方程为y=k(x-a),求出O,C到直线l的距离,从而可得d1、d2的值,利用d1、d2的比值总等于同一常数λ,建立方程,从而利用等式对任意实数k恒成立,得到三个方程,由此可得结论.
解答 解:(1)∵圆O:x2+y2=64,圆O1与圆O相交,圆O1上的点与圆O上的点之间的最大距离为21,
∴圆O1的半径为4,
∵圆心为O1(9,0),
∴圆O1的标准方程为(x-9)2+y2=16;
(2)当直线l的斜率存在时,设方程为y-b=k(x-a),即kx-y-ka-b=0
∴O,C到直线l的距离分别为h=$\frac{|ka-b|}{\sqrt{1+{k}^{2}}}$,h1=$\frac{|-9k+ka-b|}{\sqrt{1+{k}^{2}}}$,
∴d1=2$\sqrt{64-\frac{(ka-b)^{2}}{1+{k}^{2}}}$,d2=2$\sqrt{16-\frac{(-9k+ka-b)^{2}}{1+{k}^{2}}}$
∵d1与d2的比值总等于同一常数λ,
∴64-$\frac{(ka-b)^{2}}{1+{k}^{2}}$=λ2[16-$\frac{(-9k+ka-b)^{2}}{1+{k}^{2}}$]
∴[64-a2-16λ2+λ2(a-9)2]k2+2b[a-λ2(a-9)]k+64-b2-λ2(16-b2)=0
由题意,上式对任意实数k恒成立,所以64-a2-16λ2+λ2(a-9)2=0,2b[a-λ2(a-9)]=0,64-b2-λ2(16-b2)=0同时成立,
①如果b=0,则64-16λ2=0,∴λ=2(舍去负值),从而a=6或18;
∴λ=2,P(6,0),P(18,0)
②如果a-λ2(a-9)=0,显然a=9不满足,从而λ2=$\frac{a}{a-9}$,3a2-43a+192=0,△=432-4×3×192=-455<0,故方程无解,舍去;
当点P的坐标为(6,0)时,直线l的斜率不存在,此时d1=2$\sqrt{7}$,d1=$\sqrt{7}$也满足
综上,满足题意的λ=2,点P有两个,坐标分别为(6,0),(18,0),
斜率不存在时 P(18,0),直线与圆外离,舍去.
点评 本题考查圆的标准方程,考查恒成立问题,考查分类讨论的数学思想,考查学生分析解决问题的能力.

 中考解读考点精练系列答案
中考解读考点精练系列答案| A. | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | B. | $\frac{x^2}{169}-\frac{y^2}{144}=1$ | C. | $\frac{x^2}{16}+\frac{y^2}{9}=1$ | D. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | -$\frac{4}{3}$ | B. | $\frac{4}{3}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
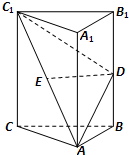 如图,在直三棱柱ABC-A1B1C1中,AB=BC,D,E分别为BB1,AC1的中点.
如图,在直三棱柱ABC-A1B1C1中,AB=BC,D,E分别为BB1,AC1的中点.