题目内容
1.已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点P(3,1),其左、右焦点分别为F1、F2,且$\overrightarrow{{F}_{1}P}$•$\overrightarrow{{F}_{2}P}$=-6,则椭圆E的离心率是( )| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{2\sqrt{2}}{3}$ |
分析 设F1(c,0),F2(-c,0),则$\overrightarrow{{F}_{1}P}$=(3-c,1),$\overrightarrow{{F}_{2}P}$=(3+c,1),利用$\overrightarrow{{F}_{1}P}$•$\overrightarrow{{F}_{2}P}$=-6,求出c,根据椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点P(3,1),可得$\frac{9}{{a}^{2}}+\frac{1}{{b}^{2}}=1$,求出a2=18,b2=2,即可求出椭圆E的离心率.
解答 解:设F1(c,0),F2(-c,0),则$\overrightarrow{{F}_{1}P}$=(3-c,1),$\overrightarrow{{F}_{2}P}$=(3+c,1),
∴$\overrightarrow{{F}_{1}P}$•$\overrightarrow{{F}_{2}P}$=9-c2+1=-6,
∴c=4,
∴a2-b2=16,
∵椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点P(3,1),
∴$\frac{9}{{a}^{2}}+\frac{1}{{b}^{2}}=1$,
∴a2=18,b2=2,
∴e=$\frac{c}{a}$=$\frac{4}{3\sqrt{2}}$=$\frac{2\sqrt{2}}{3}$,
故选:D.
点评 本题考查了椭圆的方程与性质,考查学生分析问题的能力,求出a,b,即可求出椭圆E的离心率.

练习册系列答案
相关题目
13.已知函数f(x)=sin(2x+φ)(|φ|<$\frac{π}{2}$),且f($\frac{π}{12}$)=1,为了得到g(x)=sin2x的图象,则只要将f(x)的图象( )
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
10.已知a,b∈R,则“$\sqrt{a-1}$>$\sqrt{b-1}$”是“log2a>log2b”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
 椭圆E:$\frac{{x}^{2}}{4}$+y2=1的左、右焦点分别为F1,F2,左、右顶点分别为A,B.
椭圆E:$\frac{{x}^{2}}{4}$+y2=1的左、右焦点分别为F1,F2,左、右顶点分别为A,B.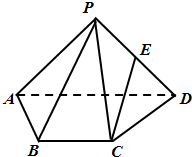 如图,四棱锥P-ABCD中,PA⊥PD,AD⊥CD,PA=PD,AD∥BC,AB=AD=2BC=2,E是棱PD的中点,设二面角P-AD-B的值为θ.
如图,四棱锥P-ABCD中,PA⊥PD,AD⊥CD,PA=PD,AD∥BC,AB=AD=2BC=2,E是棱PD的中点,设二面角P-AD-B的值为θ.