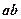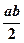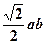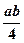题目内容
(本小题满分12分)
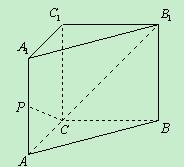
如图,在四棱锥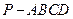 中,底面
中,底面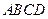 是平行四边形,
是平行四边形,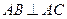 ,且
,且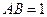 ,
,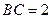 ,又
,又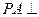 底面
底面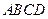 ,
,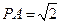 ,又
,又 为边
为边 上异于
上异于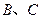 的点,且
的点,且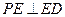 .
.
(1)求四棱锥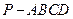 的体积;
的体积;
(2)求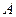 到平面
到平面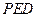 的距离.
的距离.

如图,在四棱锥
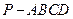 中,底面
中,底面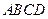 是平行四边形,
是平行四边形,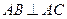 ,且
,且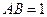 ,
,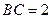 ,又
,又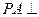 底面
底面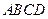 ,
,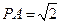 ,又
,又 为边
为边 上异于
上异于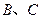 的点,且
的点,且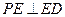 .
.(1)求四棱锥
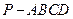 的体积;
的体积;(2)求
 到平面
到平面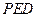 的距离.
的距离.
(1)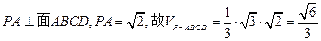
(2)A到平面PED之距为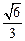
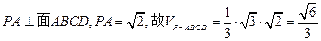
(2)A到平面PED之距为
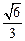
解:(1)在四棱锥P-ABCD中,ABCD是平行四边形,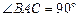
又AB=1,BC=2,则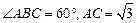
 四边形ABCD面积S=
四边形ABCD面积S=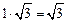
又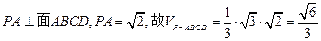 …………………(6分)
…………………(6分)
(2)
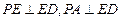 ,则
,则 ,从而
,从而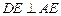
在平行四边形ABCD中,设BE=x,
则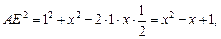
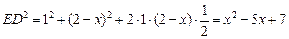
由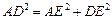 可知:
可知: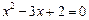 ,故
,故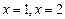 (舍)
(舍)
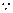
 ,故面
,故面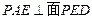 .
.
故A到面PED之距而转化为A到棱PE之距
在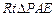 中,
中,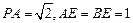
 故A到PE之距
故A到PE之距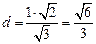
从而A到平面PED之距为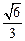 ……………………………………………(12分)
……………………………………………(12分)
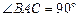
又AB=1,BC=2,则
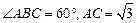
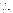 四边形ABCD面积S=
四边形ABCD面积S=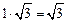
又
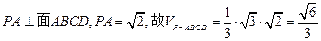 …………………(6分)
…………………(6分)(2)
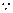
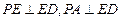 ,则
,则 ,从而
,从而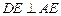
在平行四边形ABCD中,设BE=x,
则
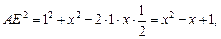
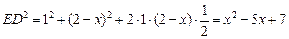
由
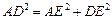 可知:
可知: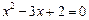 ,故
,故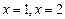 (舍)
(舍)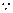
 ,故面
,故面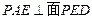 .
.故A到面PED之距而转化为A到棱PE之距
在
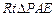 中,
中,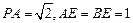
 故A到PE之距
故A到PE之距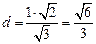
从而A到平面PED之距为
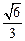 ……………………………………………(12分)
……………………………………………(12分)
练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
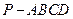 中,底面为直角梯形,
中,底面为直角梯形,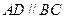 ,
,
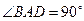 ,
,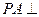 底面
底面 ,且
,且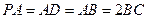 ,
,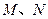 分别为
分别为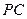 、
、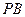 的中点。
的中点。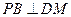 ;
;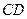 与平面
与平面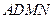 所成角的正弦值。
所成角的正弦值。
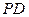 边的中点,且PA⊥底面ABCD。
边的中点,且PA⊥底面ABCD。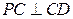

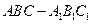 中,
中,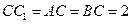 ,
,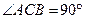 .
.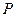 是
是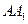 的中点,求四棱锥
的中点,求四棱锥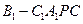 的体积.
的体积.
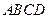 所在平面与平面四边形
所在平面与平面四边形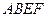 所在平面互相垂直,△
所在平面互相垂直,△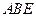 是等腰直角三角形
是等腰直角三角形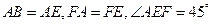
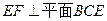 ;
;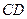 的中点为
的中点为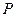 ,在直线
,在直线 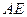 上是否存在一点
上是否存在一点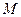 ,使得
,使得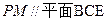 ?若存在,请指出点
?若存在,请指出点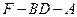 正切值的大小。
正切值的大小。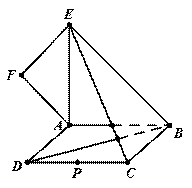
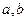 是两条不同的直线,
是两条不同的直线,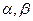 是两个不重合的平面,则下列命题中正确的是
是两个不重合的平面,则下列命题中正确的是 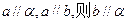
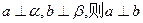
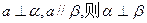
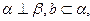 则
则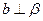
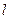 上有无数个点不在平面
上有无数个点不在平面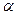 内,
内,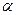
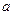 在平面
在平面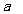 ‖
‖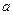 、
、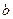 是两条不相交的直线,
是两条不相交的直线,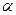 、
、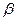 是两个相交平面,则使“直线
是两个相交平面,则使“直线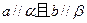
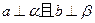
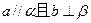
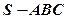 的底面边长为
的底面边长为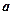 ,侧棱长为
,侧棱长为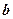 ,那么经过底边
,那么经过底边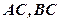 的中点且平行于侧棱
的中点且平行于侧棱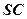 的截面面积为( )
的截面面积为( )