题目内容
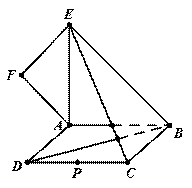
(本题满分12分) 如图,正方形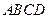 所在平面与平面四边形
所在平面与平面四边形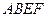 所在平面互相垂直,△
所在平面互相垂直,△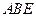 是等腰直角三角形
是等腰直角三角形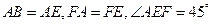
(1)求证: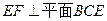 ;
;
(2)设线段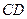 的中点为
的中点为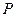 ,在直线
,在直线 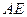 上是否存在一点
上是否存在一点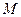 ,使得
,使得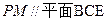 ?若存在,请指出点
?若存在,请指出点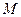 的位置,并证明你的结论;若不存在,请说明理由;
的位置,并证明你的结论;若不存在,请说明理由;
(3)求二面角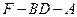 正切值的大小。
正切值的大小。
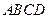 所在平面与平面四边形
所在平面与平面四边形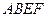 所在平面互相垂直,△
所在平面互相垂直,△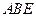 是等腰直角三角形
是等腰直角三角形
(1)求证:
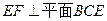 ;
;(2)设线段
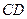 的中点为
的中点为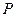 ,在直线
,在直线 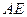 上是否存在一点
上是否存在一点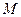 ,使得
,使得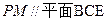 ?若存在,请指出点
?若存在,请指出点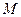 的位置,并证明你的结论;若不存在,请说明理由;
的位置,并证明你的结论;若不存在,请说明理由;(3)求二面角
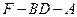 正切值的大小。
正切值的大小。
(1)略
(2)略
(3)二面角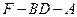 正切值为
正切值为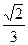
(2)略
(3)二面角
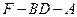 正切值为
正切值为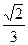
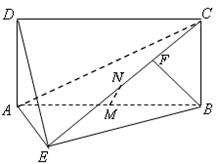
解:(Ⅰ)因为平面ABEF⊥平面ABCD,BC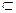 平面ABCD,BC⊥AB,平面ABEF∩平面ABCD=AB,
平面ABCD,BC⊥AB,平面ABEF∩平面ABCD=AB,
所以BC⊥平面ABEF.
所以BC⊥EF. ……………………………………2分
因为⊿ABE为等腰直角三角形,AB=AE,
所以∠AEB=45°,
又因为∠AEF=45,
所以∠FEB=90°,即EF⊥BE. …………………3分
因为BC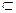 平面ABCD, BE
平面ABCD, BE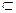 平面BCE,
平面BCE,
BC∩BE=B
所以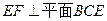 …………………………4分(II)取BE的中点N,连结CN,MN,则MN
…………………………4分(II)取BE的中点N,连结CN,MN,则MN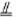
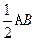
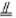 PC
PC
∴PMNC为平行四边形,所以PM∥CN. ………6分
∵CN在平面BCE内,PM不在平面BCE内,PM∥平面BCE ………8分
(III)由EA⊥AB,平面ABEF⊥平面ABCD,易知EA⊥平面ABCD.
作FG⊥AB,交BA的延长线于G,则FG∥EA.从而FG⊥平面ABCD,
作GH⊥BD于H,连结FH,则由三垂线定理知BD⊥FH.
∴ ∠FHG为二面角F-BD-A的平面角. …………………10分
∵ FA=FE,∠AEF=45°,∠AEF=90°, ∠FAG=45°.
设AB=1,则AE=1,AF=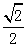 ,则
,则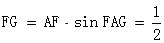
在Rt⊿BGH中, ∠GBH=45°,BG=AB+AG=1+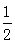 =
=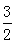 ,
,
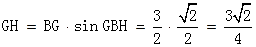 ,
, 

在Rt⊿FGH中,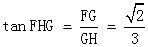 ,
,
∴ 二面角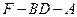 正切值为
正切值为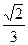 ………………12分
………………12分
 平面ABCD,BC⊥AB,平面ABEF∩平面ABCD=AB,
平面ABCD,BC⊥AB,平面ABEF∩平面ABCD=AB,所以BC⊥平面ABEF.
所以BC⊥EF. ……………………………………2分
因为⊿ABE为等腰直角三角形,AB=AE,
所以∠AEB=45°,
又因为∠AEF=45,
所以∠FEB=90°,即EF⊥BE. …………………3分
因为BC
 平面ABCD, BE
平面ABCD, BE 平面BCE,
平面BCE,BC∩BE=B
所以
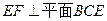 …………………………4分(II)取BE的中点N,连结CN,MN,则MN
…………………………4分(II)取BE的中点N,连结CN,MN,则MN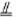
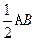
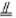 PC
PC∴PMNC为平行四边形,所以PM∥CN. ………6分
∵CN在平面BCE内,PM不在平面BCE内,PM∥平面BCE ………8分
(III)由EA⊥AB,平面ABEF⊥平面ABCD,易知EA⊥平面ABCD.
作FG⊥AB,交BA的延长线于G,则FG∥EA.从而FG⊥平面ABCD,
作GH⊥BD于H,连结FH,则由三垂线定理知BD⊥FH.
∴ ∠FHG为二面角F-BD-A的平面角. …………………10分
∵ FA=FE,∠AEF=45°,∠AEF=90°, ∠FAG=45°.
设AB=1,则AE=1,AF=
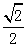 ,则
,则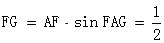
在Rt⊿BGH中, ∠GBH=45°,BG=AB+AG=1+
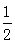 =
=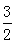 ,
,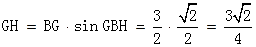 ,
, 

在Rt⊿FGH中,
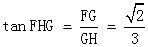 ,
,∴ 二面角
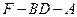 正切值为
正切值为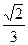 ………………12分
………………12分
练习册系列答案
相关题目

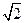 .
.
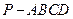 中,底面
中,底面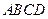 是平行四边形,
是平行四边形,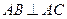 ,且
,且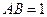 ,
,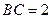 ,又
,又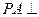 底面
底面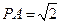 ,又
,又 为边
为边 上异于
上异于 的点,且
的点,且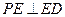 .
.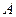 到平面
到平面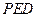 的距离.
的距离.
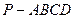 中,
中,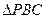 为正三角形,
为正三角形, ,
, 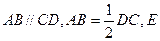 为
为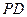 中点
中点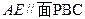 ;(2)求证:
;(2)求证:
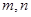 是不同的直线,
是不同的直线,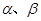 是不重合的平面,下列命题为真命题的是( )
是不重合的平面,下列命题为真命题的是( )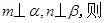
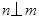
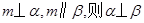
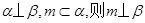
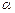 、
、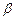 为两个确定的相交平面,a、b为一对异面直线,下列条件中能使a、b所成的角为定值的有 ( )
为两个确定的相交平面,a、b为一对异面直线,下列条件中能使a、b所成的角为定值的有 ( )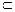
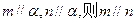
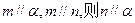

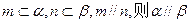
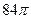 ,则圆台较小底面的半径为( )
,则圆台较小底面的半径为( )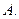 7
7  . 6
. 6 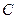 . 5
. 5  3
3