题目内容
3.已知复数z=x+yi(x,y∈R,x≠0)且|z-2|=$\sqrt{3}$,则$\frac{y}{x}$的最大值为$\sqrt{3}$.分析 直接利用是的几何意义,求解即可.
解答 解:复数z=x+yi(x,y∈R,x≠0)且|z-2|=$\sqrt{3}$,复数的几何意义是复平面内的点以(2,0)我圆心,$\sqrt{3}$为半径的圆,(x-2)2+y2=3.
则$\frac{y}{x}$的几何意义是圆上的点与坐标原点连线的斜率,
设$\frac{y}{x}=k$,即y=kx,$\frac{\left|2k\right|}{\sqrt{1+{k}^{2}}}≤\sqrt{3}$,
可得k$∈[-\sqrt{3},\sqrt{3}]$,
则$\frac{y}{x}$的最大值为:$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查复数的几何意义,直线与圆的位置关系的应用,考查计算能力.

练习册系列答案
相关题目
13.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的左右焦点分别为F1,F2,椭圆上存在点P,使得∠F1PF2=60°,则椭圆的离心率的取值范围是( )
| A. | $({0,\frac{1}{2}}]$ | B. | $[{\frac{1}{2},1})$ | C. | $({0,\frac{{\sqrt{3}}}{2}}]$ | D. | $[{\frac{{\sqrt{3}}}{2},1})$ |
11.函数f(x)=3x3-9x2+5在区间[-2,2]上的最大值是( )
| A. | 5 | B. | 2 | C. | -7 | D. | 14 |
 把正整数数列的所有数按照从小到大的原则写成如图所示的数表,第k行有k个数,第k行的第s个数(从左数起)记为A(k,s),则2015这个数可记为A(63,62).
把正整数数列的所有数按照从小到大的原则写成如图所示的数表,第k行有k个数,第k行的第s个数(从左数起)记为A(k,s),则2015这个数可记为A(63,62).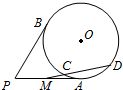 如图,P是圆O外一点,PA,PB是圆O的两条切线,切点分别为A,B,PA中点为M,过M作圆O的一条割线交圆O于C,D两点,若PB=8,MC=2,则CD=6.
如图,P是圆O外一点,PA,PB是圆O的两条切线,切点分别为A,B,PA中点为M,过M作圆O的一条割线交圆O于C,D两点,若PB=8,MC=2,则CD=6.