题目内容
15．
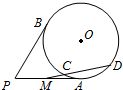如图，P是圆O外一点，PA，PB是圆O的两条切线，切点分别为A，B，PA中点为M，过M作圆O的一条割线交圆O于C，D两点，若PB=8，MC=2，则CD=6．
分析 由切割线定理，得MA2=MC•MD，结合已知中PB=8，MC=2，可得CD的值．
解答 解：由已知得MA=$\frac{1}{2}$PA=$\frac{1}{2}$PB=4，
∵MA是切线，MCD是割线，
∴MA2=MC•MD，
∵MC=2，
∴16=2×（2+CD），
解得CD=6．
故答案为：6
点评 本题考查与圆有关的线段长的求法，是基础题，解题时要认真审题，注意切割线定理的合理运用
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
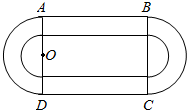某学校要建造一个面积为10000平方米的运动场．如图，运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成．跑道是一条宽8米的塑胶跑道，运动场除跑道外，其他地方均铺设草皮．已知塑胶跑道每平方米造价为150元，草皮每平方米造价为30元．
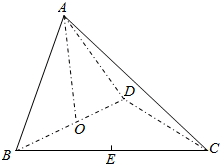如图，在三棱锥A-BCD中，O，E分别是BD，BC的中点，CA=CB=CD=BD=2，AB=AD=$\sqrt{2}$．
4．若函数y=f（x-1）的图象过点（2，3），则（ ）
| A． | f（2）=3 | B． | f（3）=2 | C． | f（1）=3 | D． | f（3）=1 |